2020 February 06 cuda

矩阵乘法的 CUDA 实现、优化及性能分析

矩阵乘法 CPU 实现

\[A_{m \times k} \cdot B_{k \times n} = C_{m \times n}\]

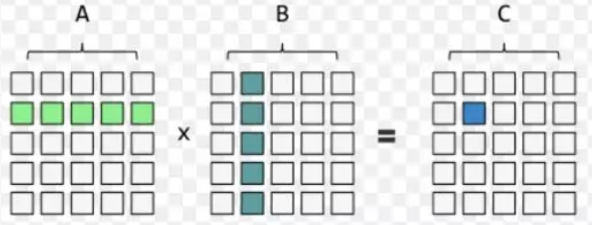
CPU程序通过三层循环实现：

void matrixMulCpu(float* fpMatrixA, float* fpMatrixB, float* fpMatrixC,
int m, int n, int k)
{
    float sum = 0.0f;
    for(int i = 0; i < m; i++)
    {
        for(int j = 0; j < n; j++)
        {
            for(int l = 0; l < k; l++)
            {
                sum += fpMatrixA[i * k + l] * fpMatrixB[l * n + j];
            }
            fpMatrixC[i * n + j] = sum;
            sum = 0.0f;
        }
    }
}

获得 C 矩阵的计算方法都是相同的, 只不过使用的是矩阵 A、B 不同的元素来进行计算, 即不同数据的大量相同计算操作, 这种计算是特别适合使用GPU来计算, 因为GPU拥有大量简单重复的计算单元, 通过并行就能极大的提高计算效率.

矩阵乘法的 GPU 常规实现使用 Global Memory

在 GPU 中执行矩阵乘法运算操作：

  1. 在 Global Memory 中分别为矩阵 A、B、C 分配存储空间.

  2. 由于矩阵 C 中每个元素的计算均相互独立, NVIDIA GPU 采用的 SIMT (单指令多线程)的体系结构来实现并行计算的, 因此在并行度映射中, 我们让每个 thread 对应矩阵 C 中1个元素的计算.

  3. 执行配置 (execution configuration)中 gridSize 和 blockSize 均有 x(列向)、y(行向)两个维度. 其中,

\[gridSize.x \times blockSize.x=n\] \[gridSize.y \times blockSize.y=m\]
  1. 每个 thread 需要执行的 workflow 为：从矩阵 A 中读取一行向量 (长度为k), 从矩阵 B 中读取一列向量 (长度为k), 对这两个向量做点积运算 (单层 k 次循环的乘累加), 最后将结果写回矩阵 C.

CUDA的kernel函数实现如下：

__global__ void matrixMulGlobalKernel(float* pfMatrixA, float* pfMatrixB, float* pfMatrixC, int m, int n, int k)
{
    int nRow = blockIdx.y * blockDim.y + threadIdx.y;
    int nCol = blockIdx.x * blockDim.x + threadIdx.x;
    float fCVal = 0.0f;

    for(int i =0; i < k; i++)
    {
        fCVal += pfMatrixA[nRow * k + i] * pfMatrixB[i * n + nCol];
    }

    pfMatrixC[nRow * n + nCol] = fCVal;
}

下面来分析一下该 kernel 函数中 A、B、C 三个矩阵对 global memory 的读取和写入情况：

读取 Global Memory：

写入 Global Memory：

由此可见：

在上述分析中, 我们是将每一个 32bit 元素 (或者说每个thread)对 global memory 的访问 (access)独立对待的. 但实际情况是如此吗, 让我们来验证下：

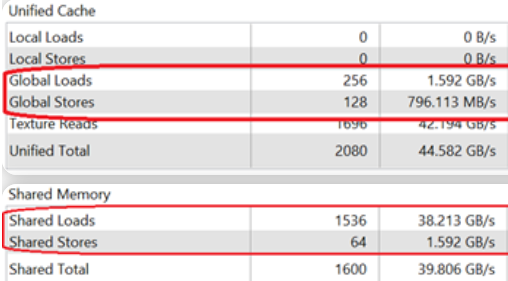
假设矩阵规模为 $m=32, n=32, k=32$, 执行配置 blockSize=(32, 32, 1), gridSize=(1, 1, 1), 使用上述的 Kernel 函数进行计算, 在 NVVP 中 Memory Bandwidth Analysis 结果如下：

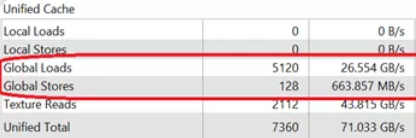
按照前面的计算方式, Global Memory Load 次数为 $32 \times 32 \times 32 \times 2=65536$ 次, Store 次数为 1024 次. 而 NVVP 显示的读取次数为 5120 次, 写入次数为 128 次, 这到底是为什么呢？

别有洞天之 Warp

GPU 编程中最重要的概念之一是 warp, 每个 warp 包含 32 个 thread, 而 GPU 的指令发射是以 warp 为最小单元的. 当 warp 中的一条指令发射一次, 称为 1 次 “transaction”, 重复发射一次, 称为 1 次 “reply”. 对于 Global Memory 的访问, warp 内的指令需要几次 transaction, 或者说是否会发生 reply, 取决于地址对齐及可合并访问的情况.

Global Memory 的读/写访问均是以 32 Byte 为单元的, 称为 1 个 segment, 即 1 transaction 可访问 32 Byte 数据 (我们假设 L1 cache 为 non-caching). 假设 1 个 warp 中的每个 thread 需要访问 1 个 32bit (=4 Byte)数据, 且访问地址是 32 Byte 对齐的, 则总共需要访问 4 个 segments, 即产生 4 次 transaction (即 3 次 reply)指令发射.

接下来我们重新分析矩阵乘法中Global Memory访问的情况：

对于前面验证矩阵, 其规模为$m=32, n=32, k=32$, 执行配置blockSize=(32,32,1), gridSize=(1,1,1),

\[m \times n \div 32 \times k \times 5=32 \times 32 \div 32 \times 32 \times 5=5120\] \[m \times n \div 32 \times 4=32 \times 32 \div 32 \times 4=128\]

我们的分析结果与 NVVP 中 GPU 实际执行结果是完全吻合的.

M/N/K/Blocksize 对计算性能的影响

M/N/K/Blocksize 对计算性能的影响

测试平台为Tesla V100-PCIE 16GB + CUDA 9.1：

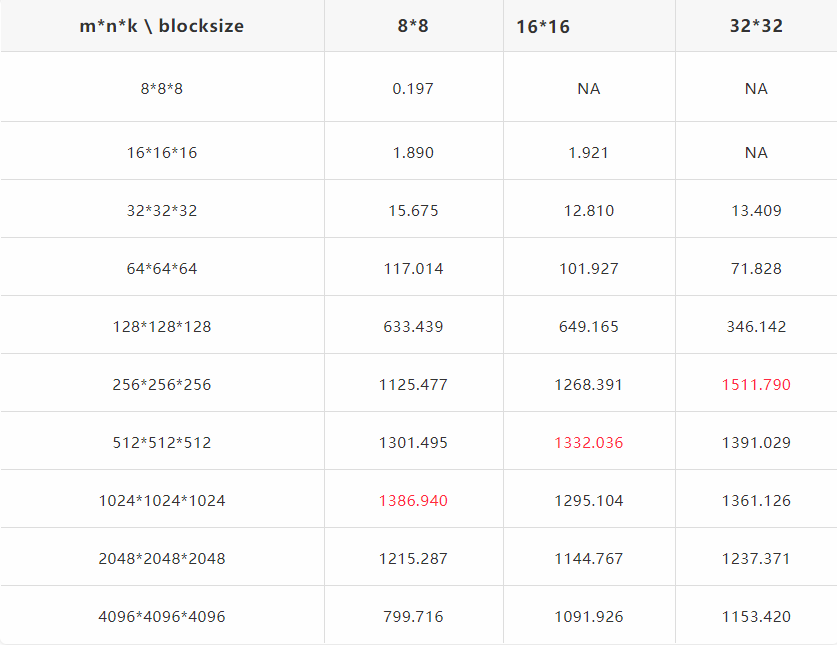
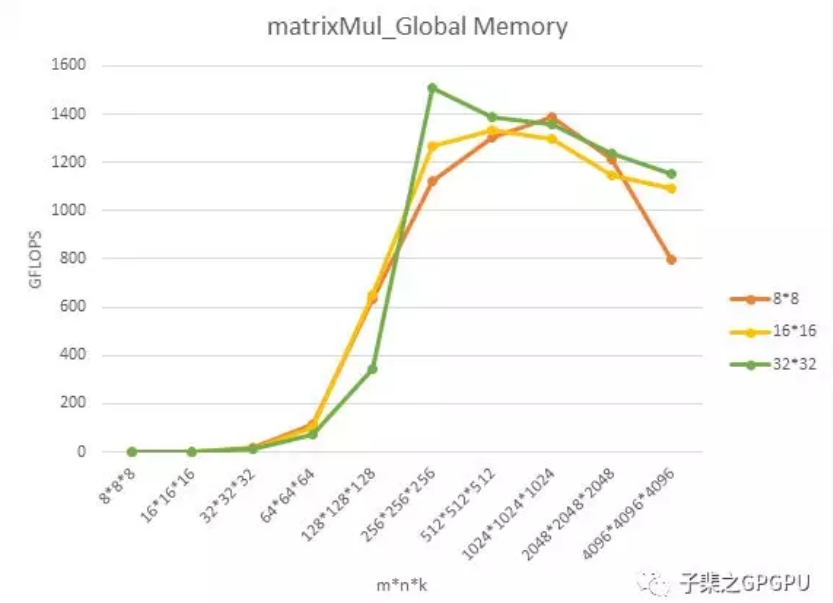
这里纵轴的GFlops（计算性能）反映的是矩阵计算的最好的计算性能，即在不停地重复该种矩阵计算时的性能峰值，其除以GPU的峰值性能极为GPU利用率。

结果分析：

Shared Memory 优化

虽然 warp 内对 Global Memory 的访问均已最大的实现了合并访问，但在 A、B 矩阵的读取操作中仍然有很多重复访问，例如，对于矩阵 A 的读取操作，通过合并访问（32 个 thread 访问 Global Memory 的同一地址，合并为一次访问），实际重复读取次数是(n/32); 对于矩阵 B 的读取操作，通过合并访问（8 个 thread 访问 32 Byte 数据可合并为一次），实际重复读取次数为(m/8)次。

在不改变这种数据读取方式的前提下又如何优化性能呢？在GPU中除了 Global Memory 还有 Shared Memory，这部分 Memory 是在芯片内部的，相较于 Global Memory 400~600 个时钟周期的访问延迟，Shared Memory 延时小 20-30 倍、带宽高 10 倍，具有低延时、高带宽的特性。因此性能优化的问题可以转变为如何利用 Shared Memory 代替 Global Memory 来实现数据的重复访问。

Shared Memory 优化原理

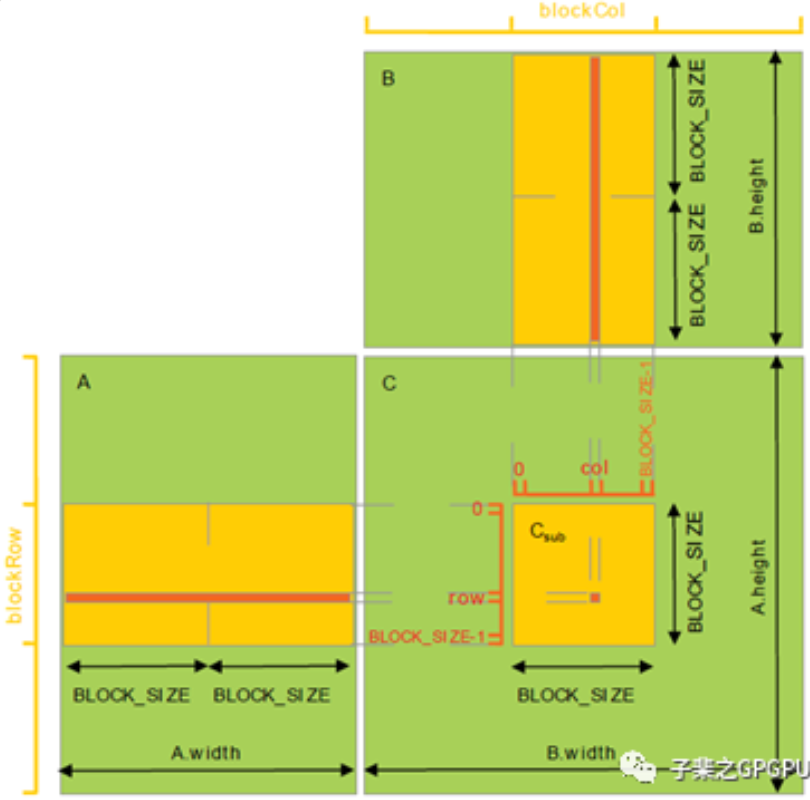
如上图所示，使用 Shared Memory 优化 Global Memory 访问的基本思想是充分利用数据的局部性。让一个 block 内的 thread 先从 Global Memory 中读取子矩阵块数据（大小为 BLOCK_SIZE*BLOCK_SIZE）并写入 Shared Memory 中; 在计算时，从 Shared Memory 中（重复）读取数据做乘累加，从而避免每次都到 Global 中取数据带来的高延迟影响。接下来让子矩阵块分别在矩阵 A 的行向以及矩阵 B 的列向上滑动，直到计算完所有k个元素的乘累加。使用 Shared Memory 优化后的 kernel 代码如下所示：

__global__ void matrixMulSharedKernel_op1(float* fpMatrixA, float* fpMatrixB,
float* fpMatrixC, int m, int n, intk)
{
    int nRow = blockIdx.y * blockDim.y + threadIdx.y;
    int nCol = blockIdx.x * blockDim.x + threadIdx.x;
    float fCVal = 0.0f;

    __shared__ float shTileA[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float shTileB[BLOCK_SIZE][BLOCK_SIZE];

    int nIter = (k + BLOCK_SIZE - 1) / BLOCK_SIZE;
    for(int i = 0; i < nIter; i++)
    {
        // load data from global memory to shared memory
        shTileA[threadIdx.y][threadIdx.x] = fpMatrixA[nRow * k + i * BLOCK_SIZE + threadIdx.x];
        shTileB[threadIdx.y][threadIdx.x] = fpMatrixB[(i * BLOCK_SIZE + threadIdx.y) * n + nCol];

        // sync to wait for all threads in one block to finish loading datas
        __syncthreads();

        // sub-matrix multiply
        for(int l = 0; l < BLOCK_SIZE; l++)
        {
            fCVal += shTileA[threadIdx.y][l] * shTileB[l][threadIdx.x];
        }

        // sync to wait for all threads in one block to finish compute
        __syncthreads();
    }

    // store results into global memory
    fpMatrixC[nRow * n + nCol] = fCVal;
}

Shared Memory 性能分析

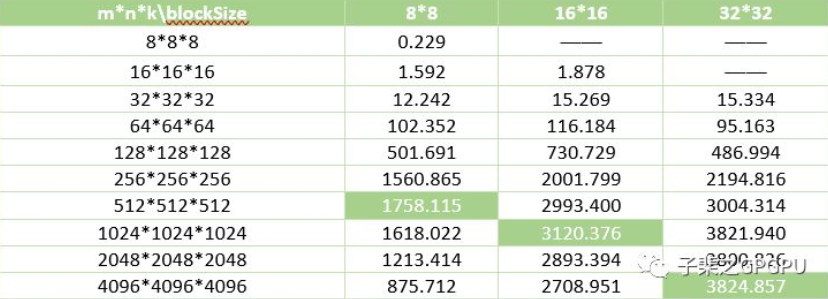
不同的blockSize(x,y)以及不同m/n/k对性能的影响，测试平台为Tesla V100-PCIE 16GB + CUDA 9.1：

Register 优化

前面的算法设计中，每个线程只计算了矩阵 C 中的一个元素，每个线程每个内层循环需要从子矩阵 A 和子矩阵 B 中各读取一个 4Byte 的元素（共取 8Byte 数据执行2次浮点运算），实际上我们可以让每个线程读取一组 Shared Memory 数据后（放入寄存器中），计算更多的元素，从而减少 Shared Memory 的访问。

// using ILP 2 to improve the performance
__global__ void matrixMulSharedILPkernel(float* fpMatrixA, float* fpMatrixB,
float* fpMatrixC, int m, int n, int k)
{
    int row = blockIdx.y * blockDim.y * 2 + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    float val[2] = {0.0f};

    __shared__ float shTileA[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float shTileB[BLOCK_SIZE][BLOCK_SIZE];

    int iter = (k + BLOCK_SIZE - 1) / BLOCK_SIZE;
    for(int i = 0; i < iter; i++)
    {
        // read data from global memory to shared memory
        shTileA[threadIdx.y][threadIdx.x] = fpMatrixA[row * k + i * BLOCK_SIZE + threadIdx.x];
        shTileA[threadIdx.y + 16][threadIdx.x] = fpMatrixA[(row + 16) * k + i * BLOCK_SIZE + threadIdx.x];

        shTileB[threadIdx.y][threadIdx.x] = fpMatrixB[(i * BLOCK_SIZE + threadIdx.y) * n + col];
        shTileB[threadIdx.y + 16][threadIdx.x] = fpMatrixB[(i * BLOCK_SIZE + threadIdx.y + 16) * n + col];

        __syncthreads();

        for(int j = 0; j < BLOCK_SIZE; j++)
        {
            val[0] += shTileA[threadIdx.y][j] * shTileB[j][threadIdx.x];
            val[1] += shTileA[threadIdx.y + 16][j] * shTileB[j][threadIdx.x];
        }

        __syncthreads();
    }

    fpMatrixC[row * n + col] = val[0];
    fpMatrixC[(row + 16) * n + col] = val[1];
}

注意, kernel launch 时的 blocksize 需要变化为: blockSize.y = BLOCK_SIZE / 2。而 gridSize 不变.

上面的 kernel 函数中，注意观察内层循环：我们让 1 个 thread 分别从子矩阵 A 中读取 2 个数据，从子矩阵 B 中读取 1 个数据（注意2次取数据是同一地址！），然后同时计算2个元素 val[0] 和 val[1]。此时，通过读取 4B*3 个数据，实现了2次乘加共4次浮点计算。减少了 shared memory 中子矩阵B一半的数据访问。

我们详细分析一下上述代码对 Shared Memory 的访问情况：

Shared Memory Store：每 1 次外层循环中对矩阵 A 和矩阵 B 有 2 次 load，总的 thread 个数减少了一半。但是实际上总的 load transactions 次数没有变化（假设 no bank conflict）。

Shared Memory Load：在每 1 次内层循环中，1 个 warp 内的 32 个 thread 需要从 shTileA 读取同 2 个元素，需要 2 次 Shared Memory Load Transactions，再从 shTileB 中读取连续的 32 个元素（假设没有 Bank Conflict，需要1次 Shared Memory Load Transactions）（注意val[0]和val[1]的计算中，shTileB 的地址是一样的），即总共需要 3 次 Shared Memory Load Transactions。$k \div \text{BLOCK_SIZE} \times \text{BLOCK_SIZE}$ 次循环总共需要 $k \times 3$ 次 Shared Memory Load Transactions。对于 $m \times n \div 2$ 个 threads，共有$m \times n \div 2 \div 32$个 warp，总共的 Shared Memory Load Transactions 数目为：$(m \times n \div 2) \div 32 \times k \times 3$。对比优化前的 Shared Memory Load Transactions 数目 $m \times n \div 32 \times k \times 2$。

当然，我们还可以继续对 kernel 函数进行优化，让每个 thread 计算的元素个数从 2 个提高到 4/8/16/32 个，对比测试结果如下（m=n=k=1024, BLOCK_SIZE=32*32）：

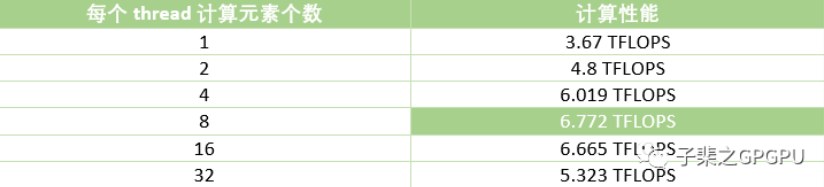
此时测出的峰值性能相比于优化前提升了约 82.5%。但是，为什么继续增大每个 thread 计算元素个数后，性能反而下降呢？一方面是继续增大该指标后，每个 block 中 thread 的个数是在减少的，但是每个 block 中需要的 Shared Memory 数量没有减少。这将导致由于 Block 总数受限，降低 SM 中的 active threads 数量，即降低了 Occupancy。另外，每个 thread 计算更多元素会使用更多的 Registers。而每个 thread 中 Registers 的个数又会反过来影响 SM 中 active threads 的个数，进而影响 Occupancy。具体 Shared Memory 或者 Registers 哪个会影响 Occupancy，取决于哪个指标先到达阈值。在没有换来同等指令集并行的情况下，Occupancy 的减少会导致计算性能受限。

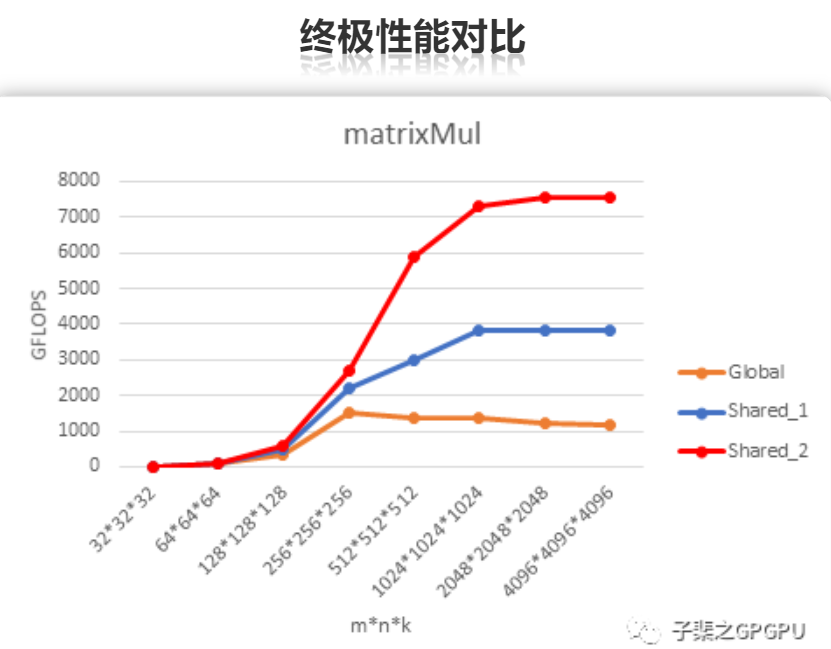
注：Shared_2代码中，每个thread计算 8 个元素。

上图为优化前后 3 个版本CUDA程序的性能差异，从图中可以得出：

All content is licensed under CC BY-NC-SA

Built with Jekyll and 3-Jekyll theme • Hosted on Github

Table of Contents