DeepLab 笔记

一、背景

DCNN 存在的问题：

1. 多次下采样使输出信号分辨率变小 —— 空洞卷积
2. 池化对输入变换具有内在空间不变性 —— CRF

二、空洞卷积

1. 作用

• 保证感受野不发生变化
• 得到密集的 feature map

2. 卷积核

\[new\_kernel = kernel + \left(kernel - 1 \right) \times \left( dilation - 1\right)\]

3. 输出大小

\[output = \left \lfloor \frac{in - kernel - \left( kernel -1\right) \times \left( dilation -1 \right) +2\times padding}{stride} \right \rfloor + 1\]

4. 感受野

\[RF_{l} = RF_{l-1} + \left( kernel\_size_{l} - 1\right) \times feature\_stride_{l-1} \times dilation_{l}\]

三、条件随机场（CRF）

作用：精细化边缘信息

DeepLab 后面接了一个全连接条件随机场 (Fully-Connected Conditional Random Fields) 对分割边界进行 refine label map。CRF 经常用于 pixel-wise 的 label 预测。把像素的 label 作为随机变量，像素与像素间的关系作为边，即构成了一个条件随机场且能够获得全局观测时，CRF 便可以对这些 label 进行建模。全局观测通常就是输入图像。

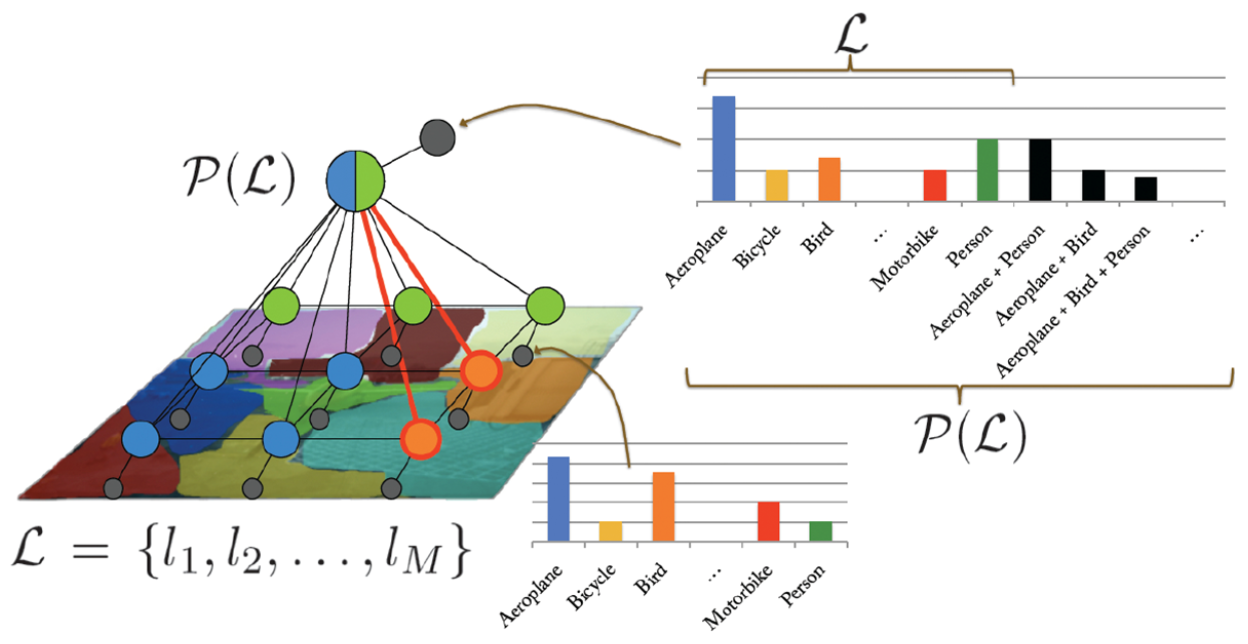
令随机变量 $X_{i}$ 是像素 i 的标签，$X_{i} \in L = l_{1}，l_{2}，\cdots，l_{L}$，令变量 $X$ 是由 $X_{1}，X_{2}，\cdots，X_{N}$ 组成的随机向量，N 就是图像的像素个数。

假设图 $G = \left(V，E\right)$，其中 $V = X_{1}，X_{2}，\cdots，X_{N}$，全局观测为$I$。条件随机场符合吉布斯分布，$\left(I，X\right)$ 可以被模型为 CRF，

\[P \left(X = x \vert I\right) = \frac{1}{Z \left(I\right) \exp \left(-E \left(x \vert I\right)\right)}\]

在全连接的CRF模型中，标签 x 的能量可以表示为：

\[E\left(x\right)=\sum_{i} \theta \left(x_{i}\right) + \sum_{ij} \theta_{i} j\left(x_{i},x_{j}\right)\]

其中，$\theta_{i}\left(x_{i}\right)$ 是一元能量项，代表着将像素 i 分成 label $x_{i}$ 的能量，二元能量项 $\varphi_{p} \left(x_{i},x_{j}\right)$ 是对像素点 i, j 同时分割成 $x_{i}，x_{j}$ 的能量。二元能量项表述像素点与像素点之间的关系，鼓励相似像素分配相同的标签，而相差较大的像素分配不同的标签，而这个“距离”的定义与颜色值和实际相对距离有关。所以这样 CRF 能够使图片尽量在边界处分割。最小化上面的能量就可以找到最有可能的分割。而全连接条件随机场的不同就在于，二元势函数描述的是每一个像素与其他所有像素的关系，所以叫“全连接”。具体来说，在 DeepLab 中一元能量项直接来自于前端 FCN 的输出，计算方式如下：

\[\theta_{i} \left(x_{i}\right) = -\log P\left(x_{i}\right)\]

而二元能量项的计算方式如下：

\[\theta_{i}j\left ( x_{i},x_{j} \right ) = \mu j\left ( x_{i},x_{j} \right )\left [ \omega_{1} \exp \left ( -\frac{\left \Vert p_{i} - p_{j} \right \Vert^{2}}{2 \sigma_{\alpha}^{2}} -\frac{\left \Vert I_{i} - I_{j} \right \Vert^{2}}{2 \sigma_{\beta}^{2}}\right ) + \omega_{2} \exp \left ( -\frac{\left \Vert p_{i} - p_{j} \right \Vert^{2}}{2 \sigma _{\gamma}^{2}} \right ) \right ]\]

其中，$\mu \left ( x_{i},x_{j} \right ) = 1$, 当 $i \neq j$ 时，其他的值为0。也就是说当标签不同是，才有惩罚。剩余表达式是在不同特征空间的两个高斯核函数，第一个基于双边高斯函数基于像素位置 p 和 RGB 值 I，强制相似 RGB 和超参数 $\sigma_{\alpha},\sigma_{\beta},\sigma _{\gamma}$ 控制高斯核函数的权重。

四、语义分割的常见结构

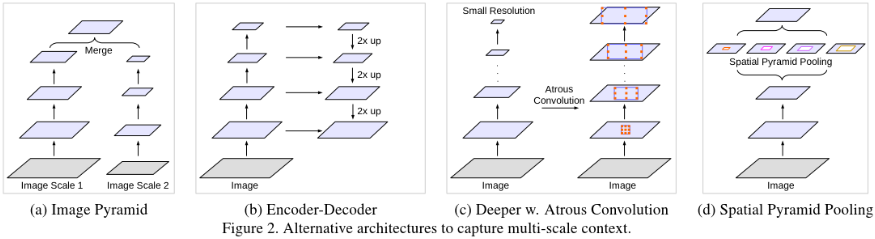
1. Image Pyramid

应用于多尺寸输入，来自小尺寸的特征响应可以编码远距离的上下文信息。较大尺寸的输入图片可以包含更多的物体细节信息。将不同尺寸的图片输入DCNN，并融合所有尺寸的feature maps。这种结构的缺点是对于较深的DCNN由于GPU的限制并不能对输入图片进行很好的scale操作。

2. Encoder-Decoder

可以获得锋利的边界，主要包含两部分：

1. 编码层feature map的空间维度降低很多，更长距离的信息在更深的编码层中更容易被捕捉到。
2. 解码层的物体细节和空间维度逐渐恢复。应用反卷积将低分辨率的feature map进行上采样。SegNet重新利用编码层中max-pooling 的 indices 和添加的卷积层来细化得到的特征。UNet是将对应层的特征信息进行拼接，并重新构造了网络。

3. Context Module

此模块包含额外的级联的模型，用于编码长距离下的语义信息。比如 Dense CRF 接到 DCNN 的后面，在 DCNN 最后一层增加几层卷积，使 CRF 和 DCNN 可以联合训练。目前，有一种普适性与稀疏性的高卷积，结合高斯条件随机场来进行分割。

4. Spatial Pyramid Pooling:

空间金字塔池化，可以池化不同分辨率的特征图来捕获丰富的上下文信息。

五、DeepLab V1

1. 关键技术

• dilation convolution
• CRF

2. 网络结构

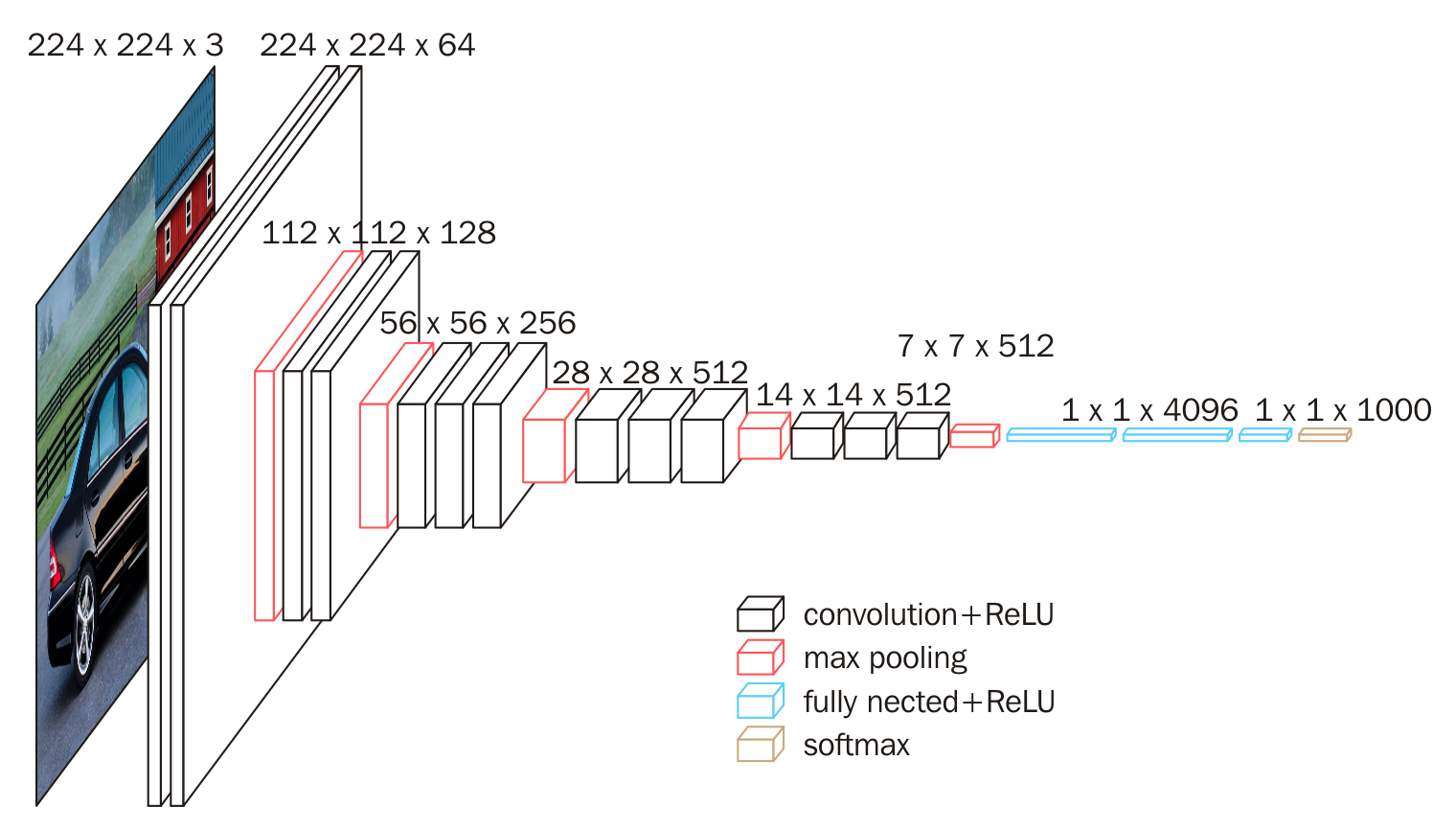
上图为 VGG16 网络，DeepLab v1 在此网络上修改。

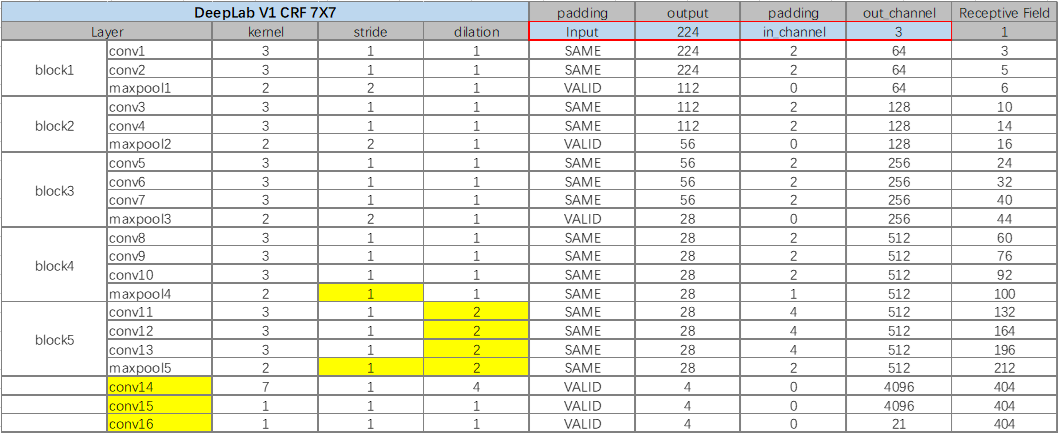
1. 全连接层替换为卷积层；

2. 去除降采样：将 pool4 和 pool5 层的 stride 由 2 改为 1，使得 VGG16 网络总的 stride 由原来的 32 变成 8。

3. 引入空洞卷积：保证感受野不变
   • pool4 stride 改变，后面的层感受野都会随之改变；
   • conv5_1，conv5_2，conv5_3，pool5 膨胀系数由 1 改为 2；
   • conv14 即 由第一个全连接层改的卷积层，膨胀系数由 1 改为 4；

4. 将最后一层的类别 1000 的分类器替换为类别 21 的一个，损失函数是卷积 output map 上每个空间位置交叉熵的求和；

5. 提升训练速度：

• 减小kernel：第一个全连接层会有 4096 个大小为 7x7 的 filters，这大大增加了计算的难度。该文减少第一个全连接层 filter 的空间尺寸（3x3），但也相对应的减少了网络的感受野，减少了 2 到 3 倍的计算时间。

• 减少channel：把 FC6 输出的 feature map 从 4096 减少到 1024

该文首先利用 DCNN 的识别能力，后接全连接的 CRF 来提高位置的准确性，通常，CRF 包含相邻节点的能量项，有利于将相同的标签分配到空间上相近的像素。本质上，short-range CRF 的作用是清除由基于局部手工设计分类器产生的错误预测。相比弱分类器，DCNN 得到的 score maps 更加平滑，此时，再使用 short-range CRF可能是有害的，因为目的不是为了平滑边界而是回复局部细节，因为经过 DCNN 后已经很平滑了。为了解决 short-range CRF 的弊端，引入了全连接CRF。

3. 实验 & 测试

• 在 ImageNet 上预训练的VGG16权重上做 finetune
• CRF 是后期处理，不参与训练
• 测试时，对特征提取后得到的 feature map 进行双线性插值，恢复到原图尺寸，然后再进行 CRF 处理。

六、DeepLab V2

1. 关键技术

• dilation convolution
• ASPP
• CRF
• poly

2. 网络结构

本文对 VGG16，ResNe-101 进行改进：

• 将全连接层变为卷积层;
• 将DCNN最后几个maxpooling去掉；
• 在后续的卷积层中添加更高 sample rate 的空洞卷积，增加特征图的分辨率；
• 对一张图片平行的使用不同 sample rate 的空洞卷积层（ASPP），增强感受野；
• 应用双线性插值将 score map 还原为原图大小;
• 全连接的 CRF，改善模型对边界的分割;

虽然CRF作为后处理的手段，但该文将CRF的 mean-filed 推理步骤进行转化，并添加到end-to-end可训练的前向网络中。

DeepLab v2 相比 DeepLab v1 的改进：对多尺寸的图片分割效果更好，引入 ASPP，用 ResNet 作为 backbone，实现比 VGG16 更好的效果。

3. ASPP

为了解决分割中的多尺寸问题，该文实验了两种方法：

1. 采用传统的方法，在训练和测试时，从 DCNN 中抽取多层（这里使三层）feature map，通过双线性插值恢复为原图尺寸，然后将其进行融合，这么做确实有效果，但是增加了DCNN的计算量。

2. 对一张图片上通过平行的进行不同尺寸的空洞卷积操作，间接的得到多尺度特性，不同 sample rate 提取的特征经过单独的后处理和融合进而生成最终的结果。采用的即 ASPP 模型，如下图。

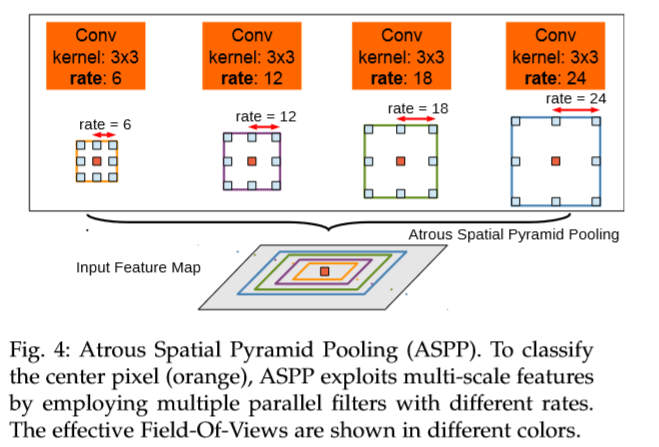
ASPP 各个空洞卷积分支采样后结果最后融合到一起（通道相同，做像素加）。

4. 实验 & 测试

将 VGG-16 和 ResNet-101 处理成分割网络。损失函数是 CNN 输出 feature map（缩小为8倍）后空间位置交叉熵的和，使用 SGD 优化算法，在 PASCAL VOC 2012, PASCAL-Context, PASCALPerson-Part,和 Cityscapes 上进行实验。

实验上的改进：

• 训练时不同的学习策略。
• ASPP
• 加深网络和多尺度处理
• 使用 poly 学习速率
• 调整 ASPP 中的rate: r={2,4,8,12} r={6,12,18,24}
• 将 VGG-16 换为 ResNet-101 使网络加深

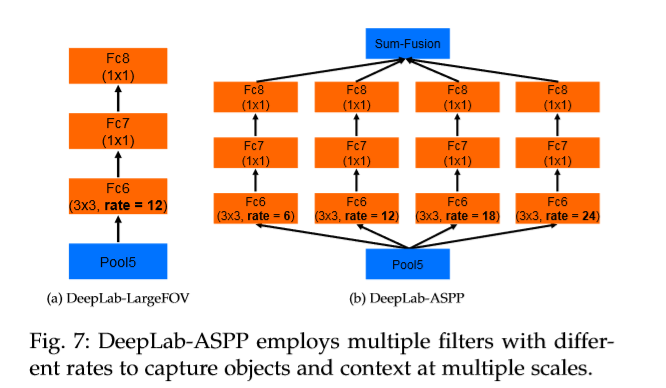
七、DeepLab V3

1. 关键技术

• dilation convolution
• 新ASPP
• poly

2. 网络结构

2.1 级联结构

作者首先以串联方式设计 artous convolution 模块。在 ResNet 的最后一个模块叫做 block4，在 block4 后复制 block4 3 次得到 block5，block6，block7，使网络加深进而可以获得更长距离的语义信息。但网络层数加深使物体的细节信息就会有损失，所以这里引入了空洞卷积。

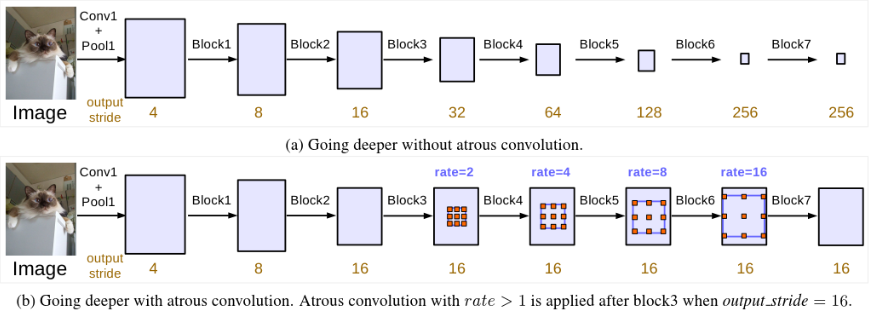
• output_stride：图像从原始分辨率到最终分辨率降低的倍数；
• 每个 block 中都包含 3 个 3×3 的卷积，除了在最后一个 block stride 为 1，剩余 block stride 都为2；
• Multi_Grid = {r1, r2, r3} 为 block4～block7 的三个 convolutional layers 的 unit rates；
• rate 的最终大小等于 Multi_Grid 与相应 rate 值的乘积。例如，当 output_stride = 16， Multi_Grid = (1,2,4) 时，block4 中 three convolutions 的 rate 分别为：rates = 2 ∗ (1, 2, 4) = (2, 4, 8)；

2.2 平行结构

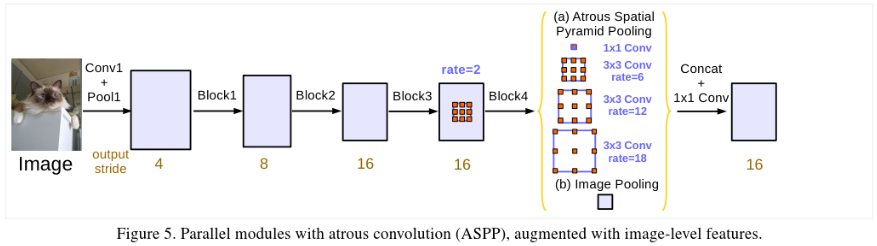
ASPP的改进：

• 无 CRF
• 增加 BN 层：加速训练；
• 增加 1x1 conv；
• 增加 global avg pool：克服远距离下有效权重减少的问题且整合全局上下文信息；

新 ASPP 的组成（output_stride=16）：

• 一个 1×1 卷积和 3 个 3×3 的空洞卷积（采样率为（6, 12, 18）），每个卷积核都有 256 个且都有 BN 层
• 图像级特征（即全局平均池化）

将所有得到的 feature map 送到，1x1x256 的卷积层中，后接 BN 层，并通过双线性插值上采样到理想分辨率。最后将所有分支得到的 feature map 进行拼接，然后送到 1x1 的卷积（自带 BN）中，最后还有一个 1x1 的卷积来产生最后的 logits。

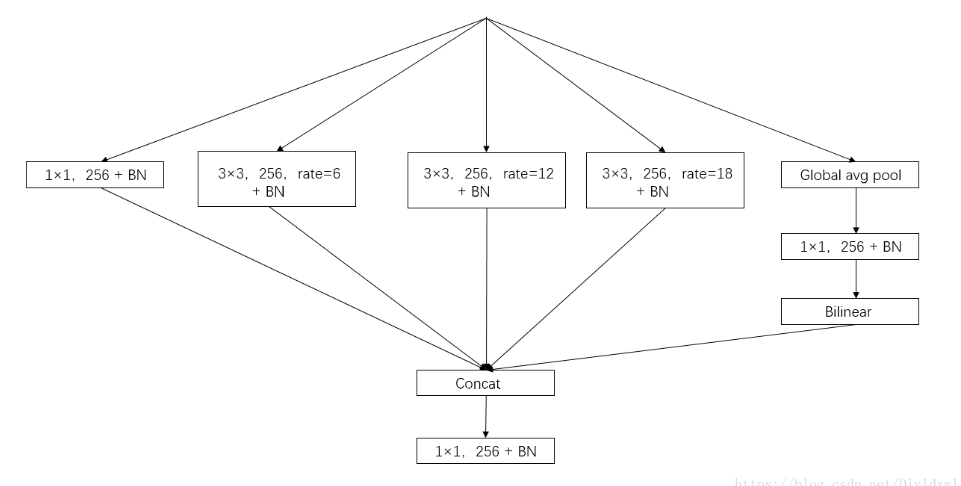
两种方法的结构合并并不会带来提升，相比较来说，ASPP 的纵式结构要好一点。所以 deeplab v3 一般也是指 ASPP 的结构。

3. 实验 & 测试

1. 学习率的更新策略和 deeplabV2 相同 —— poly；
2. 裁剪：使空洞卷积的 rate 尽可能的有效，crop 的大小裁剪为 513；
3. Batch Normalization；
4. 数据增强 —— 随机左右翻转、随机缩放；
5. Upsampling logits 保证 groundtruth 的完整性，将输出上采样 8 倍与完整的 ground Truth 进行比较；

八、DeepLab V3+

1. 关键技术

• decode module
• modify xception
• dilation convolution
• 新ASPP
• poly

2. 网络结构

在 DeepLab V3+ 中采用了 encoder-decoder 结构，在 DeepLab V3 中加入了一个简单有效的 decoder 模块来改善物体边缘的分割结果：先上采样4倍，在与encoder中的特征图 concatenate，最后在上采样 4 倍恢复到原始图像大小。除此之外还尝试使用 Xception 作为 encoder，在 ASPP 和 decoder 中应用 depth-wise separable convolution 得到了更快精度更高的网络。

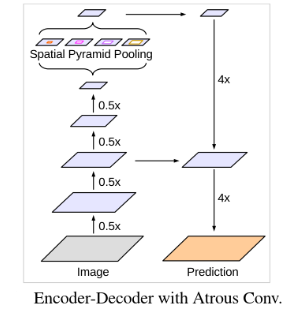
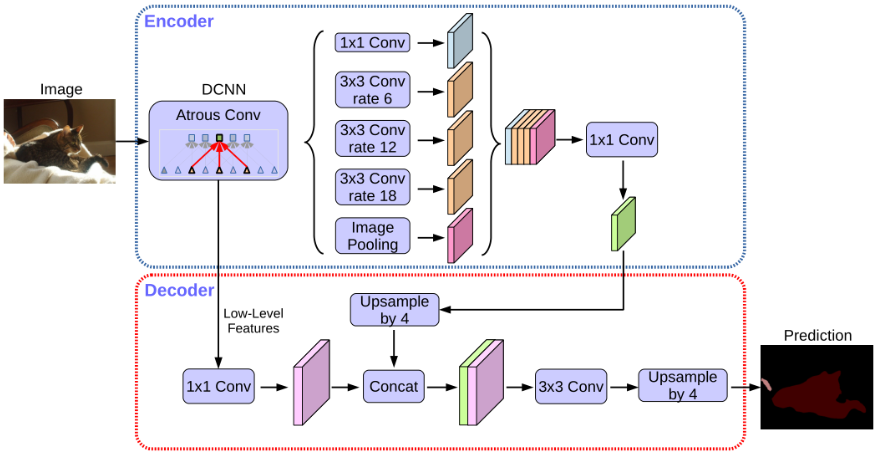
2.1 Encoder

encoder 就是 DeepLab V3，通过修改 ResNet101 最后两（一）个 block 的 stride，使得 output stride 为 8（16）。之后在 block4 后应用改进后的 ASPP，将所得的特征图 concatenate 用 1×1 的卷积得到 256 个通道的特征图。

2.2 Decoder

在 decoder 中，特征图首先上采样 4 倍，然后与 encoder 中对应分辨率低级特征 concatenate。在 concatenate 之前，由于低级特征图的通道数通常太多（256或512），而从 encoder 中得到的富含语义信息的特征图通道数只有 256，这样会淡化语义信息，因此在 concatenate 之前，需要将低级特征图通过 1×1 的卷积减少通道数。在 concatenate 之后用 3×3 的卷积改善特征，最后上采样 4 倍恢复到原始图像大小。

1. 1×1 卷积的通道数为 48；
2. 2 个 3×3 的卷积来获得更锋利的边界的 3×3 的卷积；
3. 只使用 conv2 的低级特征；

2.3 将 Xception 作为 Encoder

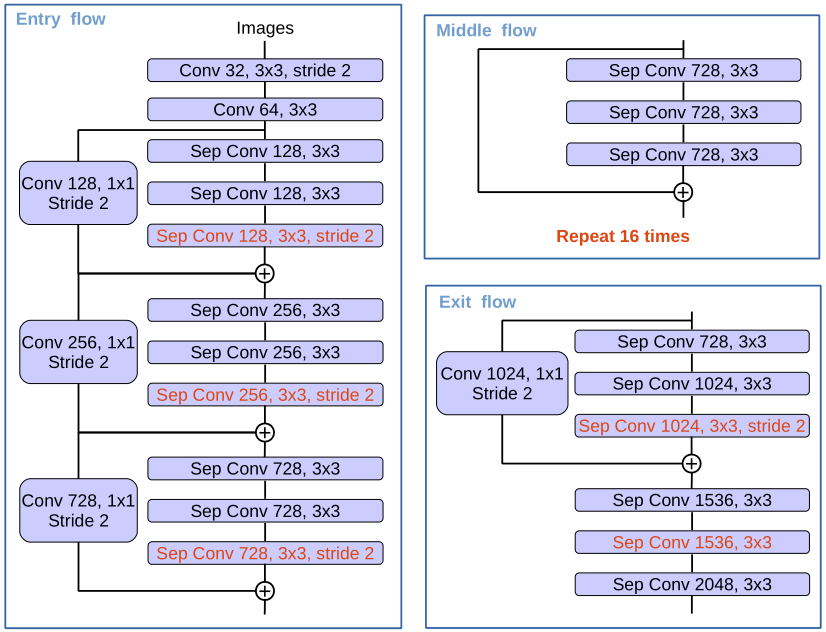
使用深度可分离卷积可极大的减少计算量，原始的 Xception 结构如下：

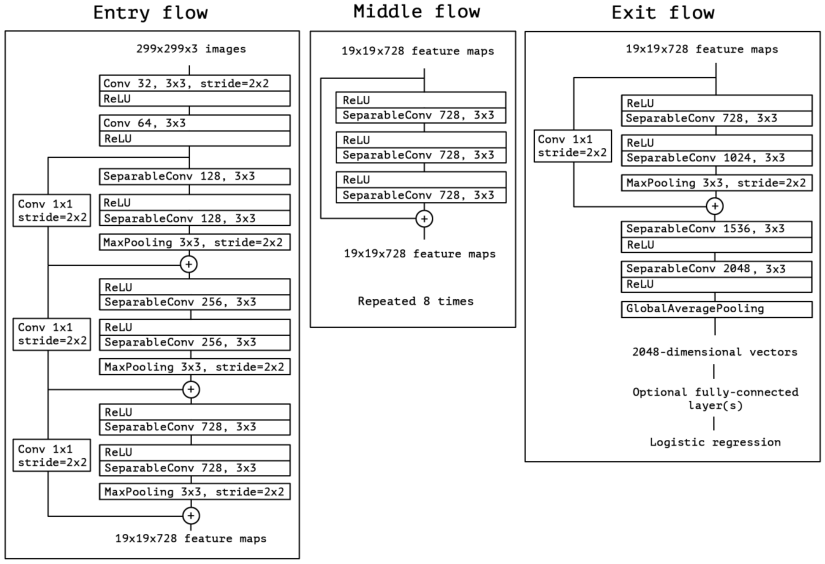
采用的 Xception 模型为 MSRA team 提出的改进的Xception，叫做 Aligned Xception，并做了几点修改：

1. Middle flow 由重复 8 次改为了 16 次，增加了网络深度；
2. 所有的 max pooling 操作替换成带 stride 的 separable convolution，这能使得对任意分辨率的图像应用 atrous separable convolution 提取特征；
3. 在每个 3×3 的 depath-wise convolution 后增加 BN 层和 ReLU；

3. 实验 & 测试

1. learning rate policy: “poly”
2. learning rate: 0.007
3. crop size: 513x513
4. output_stride = 16
5. random scale data augmentation