2018 November 27 目标检测

Fast RCNN 笔记

除了Proposal阶段，Fast RCNN基本实现了end-to-end的CNN对象检测模型

1. R-CNN、SPP-net的缺点

  1. R-CNN和SPP-Net的训练过程类似，分多个阶段进行，实现过程较复杂。这两种方法首先选用Selective Search方法提取proposals,然后用CNN实现特征提取，最后基于SVMs算法训练分类器，在此基础上还可以进一步学习检测目标的boulding box。

  2. 训练时间和空间开销大。SPP-Net在特征提取阶段只需要对整图做一遍前向CNN计算，然后通过空间映射方式计算得到每一个proposal相应的CNN特征；区别于前者，RCNN在特征提取阶段对每一个proposal均需要做一遍前向CNN计算，考虑到proposal数量较多（~2000个），因此RCNN特征提取的时间成本很高。R-CNN和SPP-Net用于训练SVMs分类器的特征需要提前保存在磁盘，考虑到2000个proposal的CNN特征总量还是比较大，因此造成空间代价较高。

  3. R-CNN检测速度很慢。RCNN在特征提取阶段对每一个proposal均需要做一遍前向CNN计算，如果用VGG进行特征提取，处理一幅图像的所有proposal需要47s；

  4. 特征提取CNN的训练和SVMs分类器的训练在时间上是先后顺序，两者的训练方式独立，因此SVMs的训练Loss无法更新SPP-Layer之前的卷积层参数，因此即使采用更深的CNN网络进行特征提取，也无法保证SVMs分类器的准确率一定能够提升。

2. Fast-RCNN 改进

  1. 训练的时候，pipeline是隔离的，先提proposal，然后CNN提取特征，之后用SVM分类器，最后再做bbox regression。Fast RCN实现了end-to-end的joint training(提proposal阶段除外)；

  2. 训练时间和空间开销大。RCNN中ROI-centric的运算开销大，所以Fast RCN用了image-centric的训练方式来通过卷积的share特性来降低运算开销；RCNN提取特征给SVM训练时候需要中间要大量的磁盘空间存放特征，Fast RCN去掉了SVM这一步，所有的特征都暂存在显存中，就不需要额外的磁盘空间了;

  3. 测试时间开销大。依然是因为ROI-centric的原因(whole image as input->ss region映射)，这点SPP-Net已经改进，Fast RCN进一步通过single scale(pooling->spp just for one scale) testing和SVD(降维)分解全连接来提速。

3. 网络框架

3.1 训练过程

  1. selective search在一张图片中得到约2k个建议窗口（Region proposal）；

  2. 将整张图片输入CNN，进行特征提取；

  3. 把建议窗口映射到CNN的最后一层卷积feature map上；

  4. 通过一个Rol pooling layer（SSP layer的特殊情况）使每个建议窗口生成固定尺寸的feature map；

  5. 利用Softmax Loss(探测分类概率) 和Smooth L1 Loss(探测边框回归)对分类概率和边框回归(Bounding box regression)联合训练（测试时候，在4之后做一个NMS）；

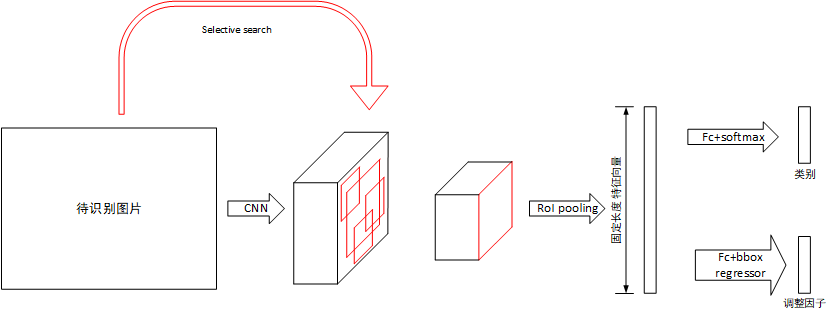
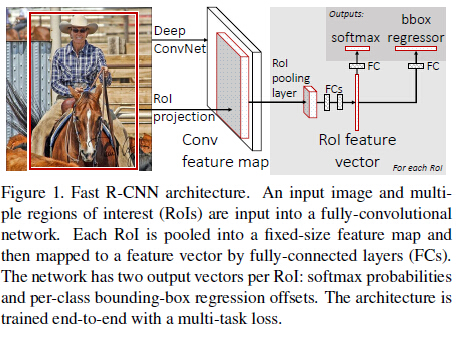
3.2 RoI pooling layer

这是SPP pooling层的一个简化版，只有一级“金字塔”，输入是N个特征映射和一组R个RoI，R»N。N个特征映射来自于最后一个卷积层，每个特征映射都是H x W x C的大小。 每个RoI是一个元组(n, r, c, h, w)，n是特征映射的索引，n∈{0, … ,N-1}，(r, c)是RoI左上角的坐标，(h, w)是高与宽。输出是max-pool过的特征映射，H’ x W’ x C的大小，H’≤H，W’≤W。对于RoI，bin-size ~ h/H’ x w/W’，这样就有H’W’个输出bin，bin的大小是自适应的，取决于RoI的大小。

3.2.1 作用

3.2.2 Roi Pooling Test Forward

Roi_pool层将每个候选区域均匀分成M×N块，对每块进行max pooling。将特征图上大小不一的候选区域转变为大小统一的数据，送入下一层。

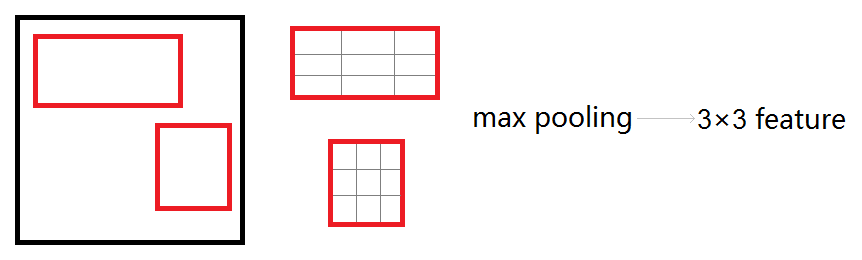
3.2.3 Roi Pooling Training Backward

首先考虑普通max pooling层。设 $x_{i}$ 为输入层的节点，$y_{j}$ 为输出层的节点。

$$\frac{\partial L}{\partial x_{i}} =\begin{cases} 0 & \delta \left ( i, j \right )= \text { false }\\ \frac{\partial L}{\partial y_{j}} & \delta \left ( i, j \right )= \text { true } \end{cases}$$

其中判决函数 $\delta \left ( i, j \right )$ 表示 i 节点是否被 j 节点选为最大值输出。不被选中有两种可能：$x_{i}$ 不在 $y_{j}$ 范围内，或者 $x_{i}$ 不是最大值。

对于roi max pooling，一个输入节点可能和多个输出节点相连。设 $x_{i}$ 为输入层的节点，$y_{rj}$ 为第 r 个候选区域的第 j 个输出节点

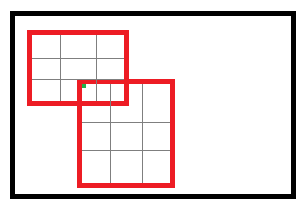
\[\frac{\partial L}{\partial x_{i}} = \sum _{r,j} \delta \left ( i, r, j \right ) \frac{\partial L}{\partial y_{rj}}\]

判决函数 $\delta \left ( i, r,j \right )$ 表示 i 节点是否被候选区域 r 的第 j 个节点选为最大值输出。代价对于 $x_{i}$ 的梯度等于所有相关的后一层梯度之和。

4. 训练过程

4.1 Pre-trained

用了3个预训练的ImageNet网络（CaffeNet/VGG_CNN_M_1024/VGG16）。预训练的网络初始化Fast RCNN要经过三次变形：

  1. 最后一个max pooling层替换为RoI pooling层，设置H’和W’与第一个全连接层兼容。(SPPnet for one scale -> arbitrary input image size )

  2. 最后一个全连接层和softmax（原本是1000个类）-> 替换为softmax的对K+1个类别的分类层，和bounding box 回归层。 (Cls and Det at same time)

  3. 输入修改为两种数据：一组N个图形，R个RoI，batch size和ROI数、图像分辨率都是可变的。

4.2 Fine-tuning

4.2.1 Multi-task loss

两个输出层，一个对每个RoI输出离散概率分布：

\[p = \left ( p_{0},\cdots , p_{K} \right )\]

一个输出bounding box回归的位移：

\[t^{k} = \left ( t_{x}^{k},t_{y}^{k},t_{w}^{k},t_{h}^{k}\right )\]

k 表示类别的索引，前两个参数是指相对于 object proposal 尺度不变的平移，后两个参数是指对数空间中相对于 object proposal 的高与宽。把这两个输出的损失写到一起：

\[L \left ( p,k^{\ast},t,t^{\ast} \right ) = L_{cls}\left ( p,k^{\ast} \right ) + \lambda \left [ k^{\ast}\geq 1 \right ] L_{loc}\left ( t,t^{\ast} \right )\]

$k^{\ast}$ 是真实类别，式中第一项是分类损失，第二项是定位损失，L 由 R 个输出取均值而来.

  1. 对于分类 loss，是一个 N+1 路的 softmax 输出，其中的N是类别个数，1是背景。SVM → softmax

  2. 对于回归 loss，是一个 4xN 路输出的 regressor，也就是说对于每个类别都会训练一个单独的 regressor，这里 regressor 的 loss 不是 L2 的，而是一个平滑的 L1，形式如下：

\[L_{loc}\left ( t,t^{\ast} \right ) = \sum_{i\in \{x,y,w,h\}} \text{smooth}_{L_{1}}\left ( t_{i},t_{i}^{\ast} \right )\]

in which

$$\text{smooth}_{L_{1}}\left (x \right )= \begin{cases} 0.5x^{2} & \text{ if } \left | x \right | < 1 \\ \left | x \right | -0.5 & \text{ otherwise } \end{cases}$$

4.2.2 Mini-batch sampling

R个候选框的构成方式如下：

类别 比例 方式
前景 25% 与某个真值重叠在 [0.5,1] 的候选框
背景 75% 与真值重叠的最大值在 [0.1,0.5) 的候选框

4.2.3 全连接层提速

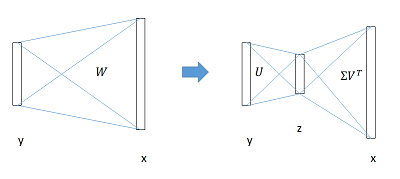
分类和位置调整都是通过全连接层(fc)实现的，设前一级数据为 x 后一级为 y，全连接层参数为 W，尺寸 $u \times v$。

一次前向传播(forward)即为：

\[y= Wx\]

计算复杂度为 $u \times v$ 。

将进行SVD分解，并用前t个特征值近似, 原来的前向传播分解成两步:

\[W = U \Sigma V^{T} \approx U\left ( :,1:t \right )\cdot \Sigma \left ( 1:t,1:t \right ) \cdot V \left ( :,1:t \right )^{T}\]

计算复杂度变为 $u \times t + v \times t$。

在实现时，相当于把一个全连接层拆分成两个，中间以一个低维数据相连。

5. 实验结论

All content is licensed under CC BY-NC-SA

Built with Jekyll and 3-Jekyll theme • Hosted on Github

Table of Contents