U-Net 笔记
医学影像分割的基石
关键点
- encode-decode 结构
- 全卷积网络
- 网络输入:overlap-tile(镜像策略)
- 跳跃结构:特征融合(拼接)
一、背景
在分割问题中,池化层的存在不仅能增大上层卷积核的感受野,而且能聚合背景同时丢弃部分位置信息。然而,语义分割方法需对类别图谱进行精确调整,因此需保留池化层中所舍弃的位置信息。
研究者提出了一种编码器-解码器 (encoder-decoder) 结构。其中,编码器使用池化层逐渐缩减输入数据的空间维度,而解码器通过反卷积层等网络层逐步恢复目标的细节和相应的空间维度。从编码器到解码器之间,通常存在直接的信息连接,来帮助解码器更好地恢复目标细节。在这种方法中,一种典型结构为 U-Net 网络。
二、 网络结构
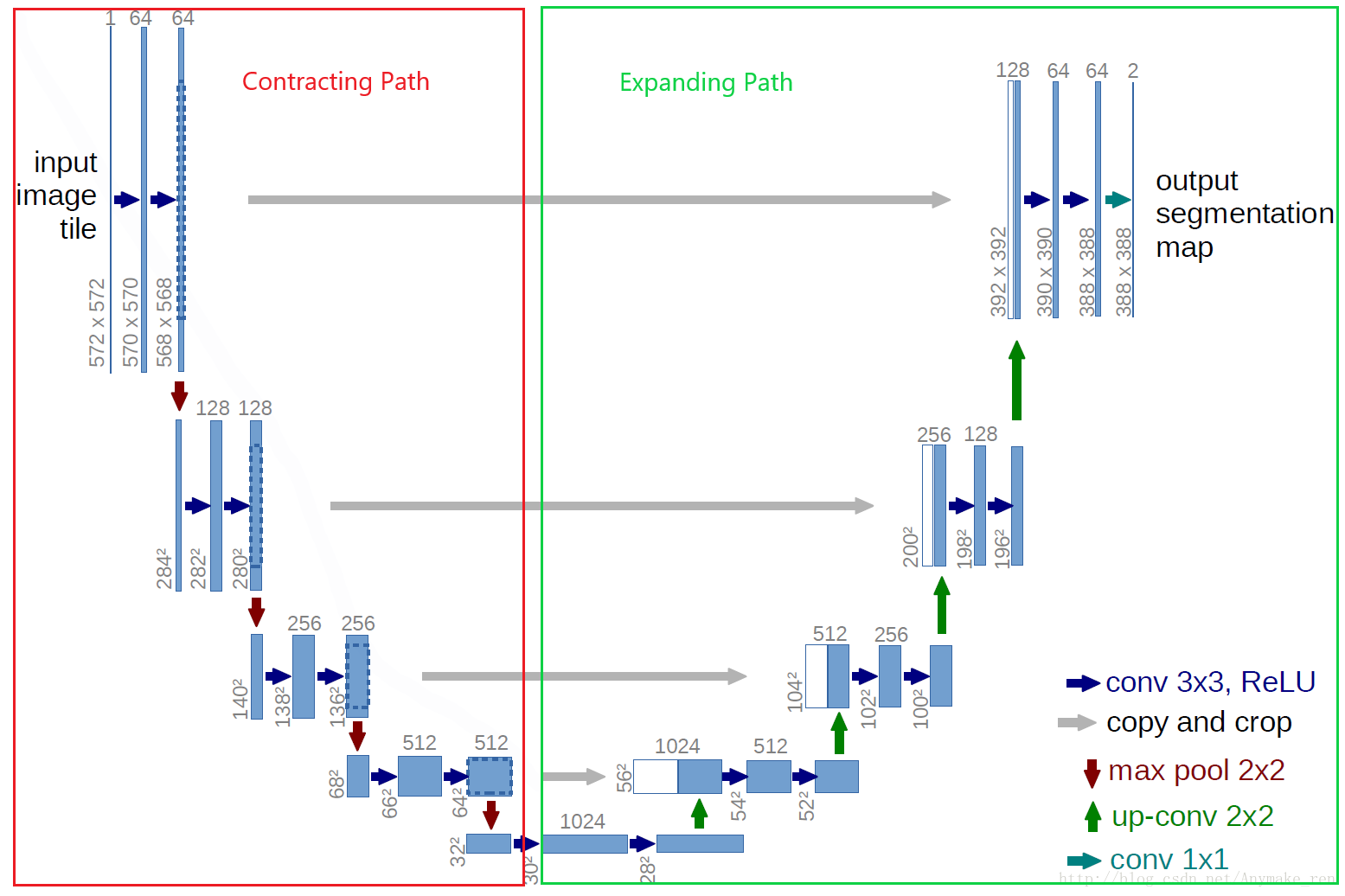
整体结构就是先编码(下采样),红色线框部分,在论文中叫做扩展路径(expansive path),再解码(上采样),绿色线框部分,在论文中叫做扩展路径(expansive path)。最终回归到跟原始图像一样大小的像素点的分类。
- 输入:572x572 的边缘经过镜像操作的图片(input image tile),原始图像是 512x512
- 输出:388x388 的 feature map,该任务是一个二分类任务,所以有两个输出 Feature Map。
-
下采样是通过max pool 2x2来进行1/2下采样的,下采样之间是两个conv卷积层,这里的卷积是使用 valid 卷积。所以在卷积过程中图像的大小是会减小的。
这会造成一个问题,就是造成了在skip connection部分concat时候大小不一致,因为在上面有一个copy & crop操作,crop就是为了将大小进行裁剪的操作。
- 上采样,相对于 FCN 的转置卷积进行上采样,这里是一个up-conv 2x2,具体对应的操作是:对行列进行2倍翻倍。
三、U-Net 与 FCN
1. 继承
U-Net 继承 FCN 的思想,继续进行改进。但是相对于FCN,有几个改变的地方,U-Net是完全对称的,且对解码器(应该自Hinton提出编码器、解码器的概念来,即将图像->高语义feature map的过程看成编码器,高语义->像素级别的分类score map的过程看作解码器)进行了加卷积加深处理,FCN只是单纯的进行了上采样。
2. Skip Connection
两者都用了这样的结构,虽然在现在看来这样的做法比较常见,但是对于当时,这样的结构所带来的明显好处是有目共睹的,因为可以联合高层语义和低层的细粒度表层信息,就很好的符合了分割对这两方面信息的需求。
3. 联合
在 FCN 中,Skip connection 的联合是通过对应像素的求和,而U-Net则是对其的 channel 的 concat 过程。
四、Overlap-tile 策略
首先,数据集我们的原始图像的尺寸都是 512x512 的。为了能更好的处理图像的边界像素,U-Net 使用了镜像操作(Overlay-tile Strategy)来解决该问题。镜像操作即是给输入图像加入一个对称的边如下图,那么边的宽度是多少呢?一个比较好的策略是通过感受野确定。因为有效卷积是会降低 Feature Map 分辨率的,但是我们希望 512x512 的图像的边界点能够保留到最后一层 Feature Map。所以我们需要通过加边的操作增加图像的分辨率,增加的尺寸即是感受野的大小,也就是说每条边界增加感受野的一半作为镜像边。
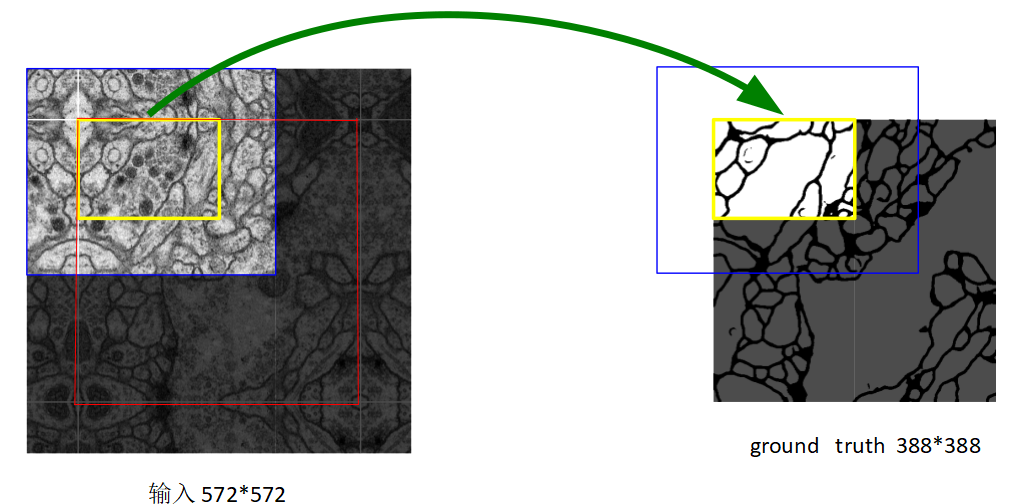
根据压缩路径的网络架构,我们可以计算其感受野:
\[rf = \left ( \left ( \left ( 0 \times 2 + 2 + 2\right ) \times 2 + 2 + 2 \right ) \times 2 + 2 + 2 \right ) \times 2 + 2 + 2 = 60\]这也就是为什么 U-Net 的输入数据是 572x572 的。572的卷积的另外一个好处是每次降采样操作的Feature Map的尺寸都是偶数,这个值也是和网络结构密切相关的。
五、损失函数
如下图所示(a)是输入数据,(b)是Ground Truth,(c)是基于Ground Truth生成的分割掩码,(d)是U-Net使用的用于分离边界的损失权值。
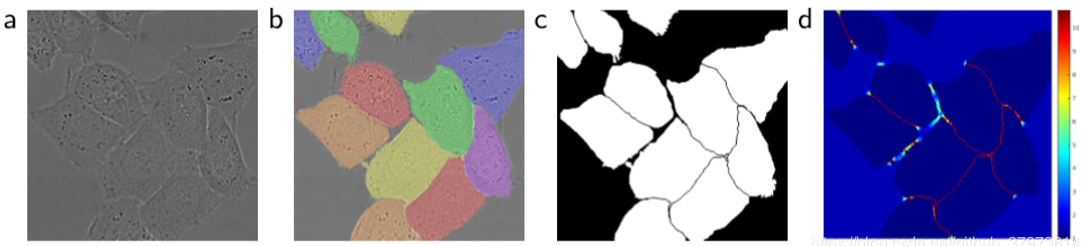
U-Net使用的是带边界权值的损失函数:
\[E = \sum_{x \in \Omega } w\left ( x \right ) \log \left ( p_{l\left ( x \right )}\left ( x \right ) \right )\]其中 $p_{l\left ( x \right )}\left ( x \right )$ 是 softmax 损失函数,$l : \Omega \rightarrow {1,\cdots,K}$ 是像素点的标签值,$\omega : \Omega \in \mathbb{R}$是像素点的权值,目的是为了给图像中贴近边界点的像素更高的权值。
\[w \left ( x \right ) = w_{c}\left ( x \right ) + w_{0} \cdot \exp \left ( - \frac{\left ( d_{1}\left ( x \right ) + d_{2}\left ( x \right ) \right )^{2}}{2 \sigma ^{2}} \right )\]其中 $\omega_{c} : \Omega \in \mathbb{R}$ 是平衡类别比例的权值,$d_{1} : \Omega \in \mathbb{R}$ 是像素点到距离其最近的细胞的距离,$d_{2} : \Omega \in \mathbb{R}$ 则是像素点到距离其第二近的细胞的距离。$\omega_{o}$ 和 $\sigma$ 是常数值,在实验中 $\omega_{o} = 10$, $\sigma = 5$。
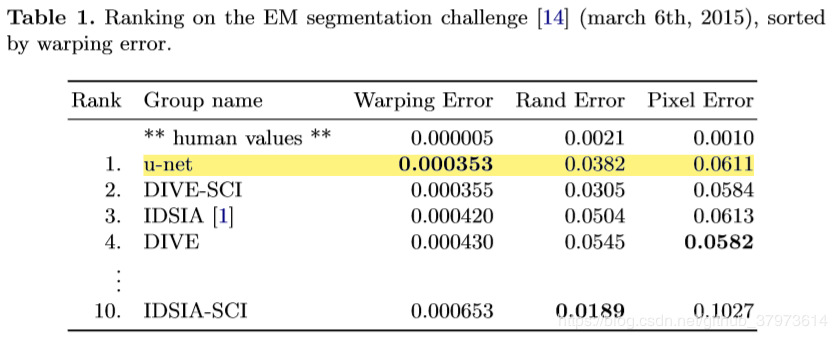
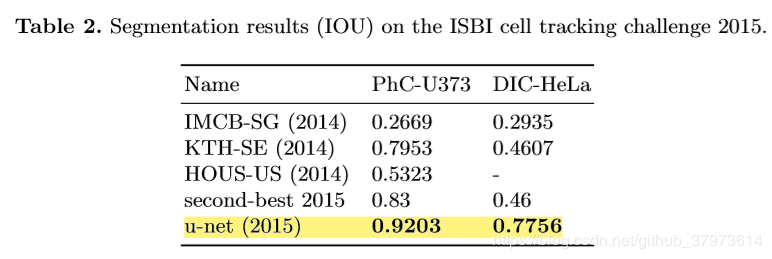
六、实验结果