条件随机场(CRF) 笔记
一、马尔可夫链
比如:一个人想从A出发到达目的地F,然后中间必须依次路过B,C, D, E,于是就有这样一个状态:
若想到达B,则必须经过A;
若想到达C,则必须经过A, B;
以此类推,最终
若想到达F,则必须经过A,B,C,D,E。
如果把上面的状态写成一个序列的话,那就是:{到达A, 到达B, 到达c, …, 到达F},而且很明显,状态序列的每个状态值取决于前面的状态是否已经满足。
于是,像这样,“状态序列的每个状态值取决于前面有限个状态”的状态序列就是马尔可夫链。
TIP:
这个名字中的“链”字用的还是很形象的,因为你可以这样理解,一条“串联在一起的灯泡”是个链子吧,那若想点亮最后一个灯泡(距离插头最远的灯泡),你必须让电流从插头起依次经过所有的灯泡。
于是,如果把上面那个状态序列 {到达A, 到达B, 到达c, …, 到达F} 中的每个状态当做灯泡的话,那这个序列就是一条“把灯泡串联在一起的链子”,如下图:

但注意:马尔可夫链的定义是“状态序列的每个状态值取决于前面有限个状态”,注意是“有限个状态”,不是“全部状态”。因此,对于马尔可夫链,其包含“想到达目的地F,则只需要到达目的地E就可以了,而前面的目的地A, B, C, D则到不到达都无所谓”这样的情况。
再注意:这里是为了便于理解而举了个“串联”的例子,真实的马尔可夫链是包含“并行”的情况,因为其定义是“状态序列的每个状态值取决于前面有限个状态”,这就包括“一个人想到达目的地C,那就得先从A处开车并在B处买早餐”这样的情况,这样一来,先到A还是先到B就无所谓了(无论是先去麦当劳买早餐再去开车,还是先开车然后在去麦当劳买早餐都行),只要A和B同时满足就好,如下图:
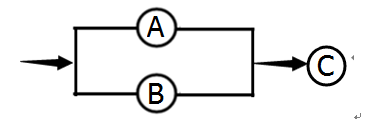
总之,马尔科夫链中的各个元素既可以是一对一,也可以是一对多,当然也可以是多对一或多对多,参照下图:
二、隐马尔可夫模型(HMM)
这里仅简单说明下HMM,详细内容见我总结的“隐马尔可夫模型(HMM) -1 ~ 4”。
还用上面一个人从A到F的例子。
但这里需要把条件和内容改一改:
条件更改:
此人想今天逛完A, B,C, D, E, F这几处,但是他想先逛哪个后逛哪个我们不知道。
内容添加:
此人每到达一处,他就会买一个礼物带给你,可这家伙逛的太兴奋了,于是乎带给你的礼物有重复的,因此,最后你会有这样的观测结果:{礼物1,礼物2,礼物1,礼物3,礼物2,礼物2} (于是还是不知道他想先逛哪个后逛哪个)。
结果,我们不知道状态序列(我们不知道他逛的顺序),但是知道观测序列,且每个观测一定是一个状态生成的(礼物一定是他到地方才能买)。
因此这个例子就是在描述:一个不知道状态序列(即马尔科夫链),却知道根据各个状态生成的一个观测随机序列的过程,而这个过程就是隐马尔可夫模型。
用数学定义说明的话就是:
隐马尔可夫模型描述由一个隐藏的马尔可夫链随机生成的不可观测的状态序列,再由各个状态生成一个观测而产生观测随机序列的过程。
OK,HMM的定义说完了,然后我们看看HMM的局限性。
HMM的局限性
1,该模型定义的是联合概率,必须列举所有观察序列的可能值,而这对多数领域来说是比较困难的。
2,基于观察序列中的每个元素都相互条件独立。即:在任何时刻观察值仅仅与状态序列中的一个状态有关。而大多数现实世界中的真是观察序列是有多个相互作用的特征和观察序列中较长范围内的元素之间的依赖而形成的。
PS:条件随机场就解决了第二个局限性。
三、产生式模型和判别式模型
如果你已经了解HMM的话就会知道:HMM中需要计算的概率是“观测序列(输入)和状态序列(输出)的联合概率”,即P(状态序列, 观测序列),即状态序列和观测序列同时发生的概率。
于是乎对于输入x(或者说观察序列)和输出y(或者说标记序列):
构建它们的联合概率分布P(y,x)的模型就是产生式模型,该模型可以根据联合概率生成样本,如:HMM, BNs, MRF。
PS:HMM是隐马尔可夫模型。
构建它们的条件概率分布P(y|x)的模型就是判别式模型,因为没有y的知识,所以无法生成样本,只能判断分类,如:CRF, SVM, MEMM。
PS:CRF就是这里要讲的条件随机场。
产生式模型:无穷样本–> 概率密度模型=产生模型–> 预测
判别式模型:有限样本–> 判别函数=预测模型–> 预测
例子 对四个元素:(1, 0),(1, 0), (2, 0), (2, 1)
产生式模型:求 P(x, y)
因为上面四个元素中(1,0)有两个,所以 P(1, 0) = 2/4 = 1/2
同理:p(1, 1) =0, p(2, 0) = 1/4, p(2, 1) = 1/4.
判别式模型:求P(y|x)
因为对上面四个元素,若x=1,那一定有y=0,所以 P(0|1) =1
同理:p(1|1) =0, p(0|2) = 1/2, p(1|2) = 1/2.
比较 产生式模型:从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度,不关心判别边界。
优点:
实际上带的信息比判别模型丰富,研究单类问题比判别模型灵活性强
能更充分的利用先验知识
模型可以通过增量学习得到
缺点:
学习过程比较复杂
在目标分类问题中易产生较大的错误率
判别式模型:寻找不同类别之间的最优分类面,反映的是异类数据之间的差异。
优点:
分类边界更灵活,比使用纯概率方法或生产模型得到的更高级。
能清晰的分辨出多类或某一类与其他类之间的差异特征
在聚类、viewpointchanges、parital occlusion and scale variations 中的效果较好
适用于较多类别的识别
缺点:
不能反映训练数据本身的特征
能力有限,可以告诉你是1还是2,但没有办法把整个场景描述出来
二者关系:
由产生式模型可以得到判别模型,反之不能。
四、条件随机场(CRF)
好了,终于到CRF了,那什么是CRF呢?
这里再举个例子:
假设你基(姬)友给了你ta一天生活的照片(这些照片是排好序的),然后让你给这些照片打上标签(Tag),比如:这张在吃饭,这张在睡觉,这张在唱歌,那么你该怎么做呢?
如果用HMM的思想,那就是:
我手上已经有了观测集合(一天的照片),然后让我求该观测集合对应的状态集合(打Tag)。OK,我开始打Tag了,嗯….这张照片黑乎乎的,那可能在睡觉;这张照片七彩斑斓的,是在KVM吧,那是在唱歌;这张….这张张着大嘴的特写是什么鬼?在吃饭?在唱歌?嗯….看不懂。问问ta好了,(转头),诶?ta人呢?我特!!算了,胡乱给一个!在狼嚎(唱歌)!嗯,就这么愉快的决定了。
于是乎像上面这个例子描述的这样,虽然HMM最终会给出一个结论,但因为HMM的“基于观察序列中的每个元素都相互条件独立”的缺陷,导致其在给某个观测“配对”状态时会毫无根据。
不过我们是人,我们才不会傻乎乎的胡乱猜,那在这样的情况下我们怎么做?答案大家都知道:我们会看看前一张图片是什么,如果前一张图片是在KVM,那这张就很有可能在唱歌;如果前一张是在厨房,那这一张就很有可能在张嘴吃饭。
根据这个例子,我们可以看出,在给某个输出(观测/特征)找其输入(产生“观测/特征”的状态)时,不能不考虑上下文(紧挨着该特征的特征),否则准确性会大大降低。
而这种“HMM强化版的思想”就是CRF了。
好了,下面让我们对比着HMM一步步的理清CRF。
CRF与HMM
首先,我们先把上面的例子简单切换一下:“照片”切换成“单词”,“照片的Tag”切换成“词性标签”(如:名词、动词、形容词等),“给照片打Tag”切换成“词性标注”(即:这个词是名词?动词?还是什么)
而上面在介绍“产生式模型和判别式模型”时说明了CRF属于判别式模型,而这里再详细些,即CRF的本质是:“隐含变量(这里磁性标签是隐含变量)的马尔科夫链” + “可观测状态到隐含变量”的条件概率。
好了,下面开始。
PS:后面的“词性标签”和“词语”分别对应“隐含变量,即输入”和“观测状态,即输出”。
先说马尔科夫链部分:
假设CRF和HMM的词性标签都满足马尔科夫性,即,当前词性仅和上一个词有概率转移关系而与其他位置的词性无关,比如:形容词后面跟形容词的概率是0.5,跟修饰性“的”的概率为0.5,跟动词的概率为0。
因此,通过在一个标注集上进行统计,就很容易得到一个概率转移矩阵,即任意词性A后紧邻任意词性B的概率都可以被统计出来。
对HMM来说,这部分就结束了。
但对CRF来说,它在二维的条件转移矩阵的基础上又增加了一维词语特征,如:当AB紧邻,A是动词且单词的长度超过3时,B是名词的概率是xx。
在这个小例子中在判断B时仅考虑一个词A,即统计P(B|A),这当然能够得到很多数据的反馈,而如果在判断B时需要考虑多个词呢?如P(B|ASDFGH),那这就可能会遇到数据稀疏的问题,因为序列ASDFGH根本就没有在数据集中出现过。注意数据稀疏对机器学习的影响是巨大的,因此马尔科夫链在CRF这边会以损失一定的全局信息来换取更饱满的数据,实验证明这笔交易在词性标注时是赚的。
再说词性(隐含变量,即输入)和词语(观测状态,即输出)的映射概率:
如果是HMM,那就是统计所有的词性组合,然后计算这所有的词性组合生成该单词组合的概率,然后选一个概率最大的词性组合。
而CRF正好反过来,CRF通过对挖掘词语本身的特征,把词语转换为一个k维特征向量,然后对于每个特征计算特征到词性的条件概率,这样每个词语对候选词性的条件概率即为所有特征条件概率的加和。比如我们假设特征向量只有两个,且P (”词语长度>3”–>名词词性)的概率为0.9, P (“词语位于句子末尾“–> 名词词性)概率为0.4,且一个词恰好满足这两个特征,则其为名词的条件概率为 (0.9 + 0.4) / 2 = 0.65。这样,CRF根据这个条件转移数值再结合词性的马尔科夫特性,就可以使用与HMM类似的方法寻找最优的词性标注序列了。
五、概率无向图模型/马尔可夫随机场(MRF)
模型定义 首先是无向图。那什么是无向图呢?
其实无向图就是指没有方向的图….我没有开玩笑,无向图真是这玩意。只不过这里我们研究的无向图的细节是:这个图是有节点和连接节点的边组成的集合,像下面这样:
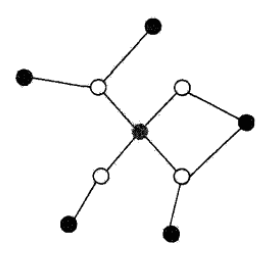
然后上面的节点表示一个个随机变量,边表示随机变量之间的依赖关系。
为了方便用数学语言描述,我们把节点和边分别记作v和e,节点和边的集合分别记作V和E,于是图就记作G=(V, E)。
无向图清楚了,那什么是概率无向图模型?是这样。
假设有联合概率分布P(Y),Y是属于某个集合的一组随机变量。如果用无向图G=(V, E)表示概率分布p(Y)的话,那在图G中,节点v∈V就表示一个随机变量Yv, Y = (Yv)v∈V;边e∈E表示随机变量之间的概率依赖关系。而如果P(Y)满足成对、局部或全局马尔可夫性的话,就称此联合概率分布为概率无向图模型,或马尔可夫随机场。
那么问题来了:什么是“成对、局部、全局马尔可夫性”。
成对马尔可夫性:
设u和v是无向图G中任意两个没有边连接的节点,节点u和v分别对应随机变量Yu和Yv。其他所有节点为O,对应的随机变量是Yo。成对马尔可夫性是指给定随机变量组Yo的条件下随机变量Yu和Yv是条件独立的,即
P(Yu,Yv|Yo) = P(Yu|Yo)P(Yv|Yo)
局部马尔可夫性:
设v∈V是无向图G中任意一个节点,W是与v有边连接的所有节点,O是v、W以外的其他所有节点。v表示随机变量是Yv,W表示的随机变量组是YW,O表示的随机变量组是Yo。局部马尔可夫性是指在给定随机变量组YW的条件下随机变量Yv与随机变量组Yo是独立的,即
P(Yu,Yv|Yw) = P(Yv|Yw)P(Yo|Yw)
在 P(Yo|YW)> 0时,等价地,
P(Yv|Yw)= P(Yv|Yw, Yo)
全局马尔可夫性:
设节点集合A,B是在无向图G中被节点集合C分开的任意节点集合,如下图所示:
节点集合A,B和C所对应的随机变量组分别是YA,YB,YC。全局马尔可夫性是指给定随机变量组YC条件下随机变量组YA和YB是条件独立的,即
P(YA,YB| YC) = P(YA|YC)P(YB|YC)
好了,那下面让我们再次总结下概率无向图模型。
概率无向图模型:
假设有联合概率分布P(Y),用无向图G=(V, E)表示,在图G中,节点表示随机变量;边表示随机变量之间的概率依赖关系。如何联合概率分布P(Y)满足成对、局部或全局马尔可夫性的话,就称此联合概率分布为概率无向图模型,或马尔可夫随机场。
以上是概率无向图模型的定义,而实际上,我们更关心如何求其联合概率分布P(Y)。于是,为了求解给定的概率无向图模型,我们希望将整体的联合概率写成若干个子联合概率的乘积形式,也就是将概率进行因子分界,这样便于模型的学习与计算。而事实上,概率无向图模型的最大特点就是便于因子分解。
概率无向图模型的因子分解 首先介绍因子分解时需要了解的两个概念:团与最大团。
团:无向图G中任何两个结点均有边连接的节点子集成为团。
最大团:若C是无向图G的一个团,并且不能再加进任何一个G的节点使其成为一个更大的团,则称此C为最大团。
如下图所示:
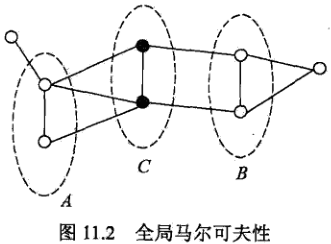
图11.3表示由4个节点组成的无向图。图中有2个节点组成的团有5个:{Y1, Y2},{Y2, Y3}, {Y3, Y4}, {Y4, Y2}, {Y1, Y3}。有两个最大团:{Y1, Y2, Y3和{Y2, Y3, Y4}。而{Y1, Y2,Y3, Y4}不是一个团,因为Y1和Y4没有边连接。
于是,将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解。
好了,需要了解的定义了解了,那我们就看看如何把这些定义用到联合概率P(Y)上。
给定概率无向图模型,设其无向图为G,C为G上的最大团,YC表示C对应的随机变量。那么概率无向图模型的联合概率分布P(Y)可写作图中所有最大团C上的函数ΨC(YC)的乘积形式,即: