图像的上采样

一、上采样原理

图像放大几乎都是采用内插值方法，即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。

二、上采样的方法

2.1 插值法 - Interpolation

最简单的方式是重采样和插值：将输入图片 input image 进行 rescale 到一个想要的尺寸，而且计算每个点的像素点，使用如双线性插值 (Bilinear-Interpolation) 等插值方法对其余点进行插值。

在AlexNet中就使用了较合适的插值方法。各种插值方法都有各自的优缺点。插值就是在不生成像素的情况下增加图像像素大小的一种方法，在周围像素色彩的基础上用数学公式计算丢失像素的色彩（也有的有些相机使用插值，人为地增加图像的分辨率）。所以在放大图像时，图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。

2.1.1 最邻近元法 - Nearest Neighbour Interpolation

这是最简单的一种插值方法，不需要计算，在待求象素的四邻象素中，将距离待求象素最近的邻象素灰度赋给待求象素。设 i+u, j+v (i, j为正整数， u, v为大于零小于1的小数，下同)为待求象素坐标，则待求象素灰度的值 f(i+u, j+v)　如下图所示：

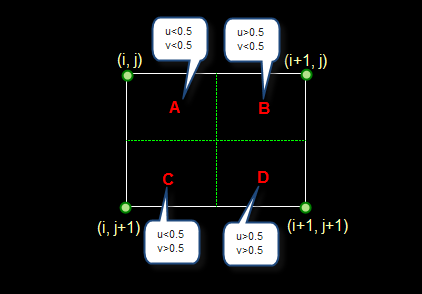
如果 (i+u, j+v) 落在A区，即 u<0.5, v<0.5，则将左上角象素的灰度值赋给待求象素，同理，落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。

最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。当图片放大时，缺少的像素通过直接使用与之最接近的原有的像素的颜色生成，也就是说照搬旁边的像素，这样做的结果是产生了明显可见的锯齿。

2.1.2 双线性内插法 - Bilinear Interpolation

双线性插值是通过周边的四个点，计算权值，然后决定插入后的图像的像素值。新生成的图像中每个点都会计算一遍，是利用待求象素四个邻象素的灰度在两个方向上作线性内插，如下图所示：

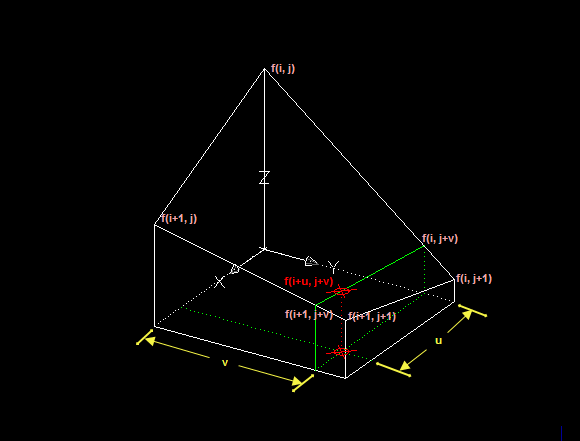
对于 (i, j+v)，f(i, j) 到 f(i, j+1) 的灰度变化为线性关系，则有：

\[f\left(i, j+v\right) = \left[ f\left(i, j+1\right) - f\left(i, j\right) \right] * v + f\left(i, j\right)\]

同理对于 (i+1, j+v) 则有：

\[f\left(i+1, j+v\right) = \left[ f\left(i+1, j+1\right) - f\left(i+1, j\right) \right] * v + f\left(i+1, j\right)\]

从 f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系，由此可推导出待求象素灰度的计算式如下：

\[f\left(i+u, j+v\right)=\left(1-u\right)*\left(1-v\right)*f\left(i, j\right)+\left(1-u\right)*v*f\left(i, j+1\right)+u*\left(1-v\right)*f\left(i+1, j\right)+u*v*f\left(i+1, j+1\right)\]

双线性内插法的计算比最邻近点法复杂，计算量较大，但没有灰度不连续的缺点，结果基本令人满意。双线性插值算法（Bilinear Interpolation）输出的图像的每个像素都是原图中四个像素（2×2）运算的结果，这种算法极大地消除了锯齿现象它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊。

2.1.3 三次内插法

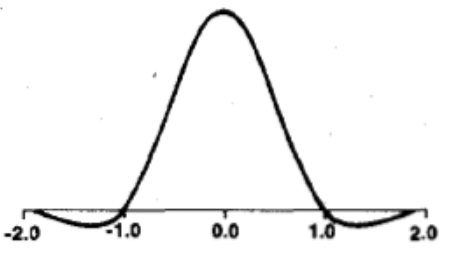
该方法利用三次多项式 $S\left ( x \right )$ 求逼近理论上最佳插值函数$\frac{\sin\left ( x \right )}{x}$, 其数学表达式为：

$$ W\left(x\right)= \begin{cases} \left(a+2\right)\left|x\right|^{3}-\left(a+3\right)\left|x\right |^{2}+1 & \text{ for } \left|x\right|\leqslant1 \\ a\left|x\right|^{3}-5a\left|x\right|^{2}+8a\left|x\right|-4a & \text{ for } 1<\left|x\right|<2 \\ 0 & \text{ otherwise } \end{cases} $$

其中，a取-0.5.该函数形状如下：

待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到，如下图：

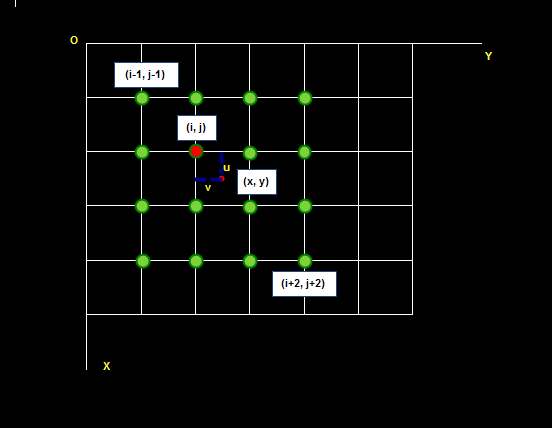
待求像素的灰度计算式如下：$f\left(x,y\right) = f\left(i+u,j+v\right)=ABC$

其中:

$$ A = \begin{vmatrix} S\left ( 1 + v \right ) \\ S\left ( v \right ) \\ S\left ( 1 - v \right ) \\ S\left ( 2 - v \right ) \end{vmatrix}^T $$

$$ B = \begin{vmatrix} f\left ( i-1,j-1 \right ) & f\left ( i-1,j \right ) & f\left ( i-1,j+1 \right ) & f\left ( i-1,j+2 \right )\\ f\left ( i,j-1 \right ) & f\left ( i,j \right ) & f\left ( i,j+1 \right ) & f\left ( i,j+2 \right )\\ f\left ( i+1,j-1 \right ) & f\left ( i+1,j \right ) & f\left ( i+1,j+1 \right ) & f\left ( i+1,j+2 \right )\\ f\left ( i+2,j-1 \right ) & f\left ( i+2,j \right ) & f\left ( i+2,j+1 \right ) & f\left ( i+2,j+2 \right ) \end{vmatrix} $$

$$ C = \begin{vmatrix} S\left ( 1 + u \right ) \\ S\left ( u \right ) \\ S\left ( 1 - u \right ) \\ S\left ( 2 - u \right ) \end{vmatrix} $$

三次曲线插值方法计算量较大，但插值后的图像效果最好。

2.2 反卷积 - Deconvolution

反卷积，是卷积的逆过程，实现上采用转置卷积核的方法，又称作转置卷积 (transposed convolution)。为实现 deconvolution，直接使 deconv 的前向传播模拟 conv 的反向传播。

举个栗子：4x4的输入，卷积Kernel为3x3, 没有 Padding / Stride, 则输出为2x2。

输入矩阵可展开为16维向量，记作 x

输出矩阵可展开为4维向量，记作 y

卷积运算可表示为 y = Cx

不难想象 C 其实就是如下的稀疏阵:

$$ \begin{vmatrix} \omega_{0,0} & \omega_{0,1} & \omega_{0,2} & 0 & \omega_{1,0} & \omega_{1,1} & \omega_{1,2} & 0 & \omega_{2,0} & \omega_{2,1} & \omega_{2,2} & 0 & 0 & 0 & 0 & 0 \\ 0 & \omega_{0,0} & \omega_{0,1} & \omega_{0,2} & 0 & \omega_{1,0} & \omega_{1,1} & \omega_{1,2} & 0 & \omega_{2,0} & \omega_{2,1} & \omega_{2,2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \omega_{0,0} & \omega_{0,1} & \omega_{0,2} & 0 & \omega_{1,0} & \omega_{1,1} & \omega_{1,2} & 0 & \omega_{2,0} & \omega_{2,1} & \omega_{2,2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \omega_{0,0} & \omega_{0,1} & \omega_{0,2} & 0 & \omega_{1,0} & \omega_{1,1} & \omega_{1,2} & 0 & \omega_{2,0} & \omega_{2,1} & \omega_{2,2} \end{vmatrix} $$

平时神经网络中的正向传播就是转换成了如上矩阵运算。

那么当反向传播时又会如何呢？首先我们已经有从更深层的网络中得到的$\frac{\partial Loss}{\partial y}$

$$ \frac{\partial Loss}{\partial x_j} = \sum_{i}\frac{\partial Loss}{\partial y_i}\frac{\partial y_i}{\partial x_j} = \sum_{i}\frac{\partial Loss}{\partial y_i}C_{i,j} = \frac{\partial Loss}{\partial y} \cdot C_{\ast ,j} = C_{\ast ,j}^{T}\frac{\partial Loss}{\partial y} $$

回想第一句话，你猜的没错，所谓逆卷积其实就是正向时左乘 $C^{T}$ ，而反向时左乘 $\left(C^{T}\right)^{T}$，即 C 的运算。

FCN 的 upsampling 过程，就是把 feature map，abcd进行一个反卷积，得到的新的 feature map 和之前对应的 encoder feature map 相加。

2.3 反池化 - unPooling

反池化，在池化过程中，记录下max-pooling在对应kernel中的坐标，在反池化过程中，将一个元素根据kernel进行放大，根据之前的坐标将元素填写进去，其他位置补0。 unPooling是在CNN中常用的来表示max pooling的逆操作。

三、上采样三种方法对比

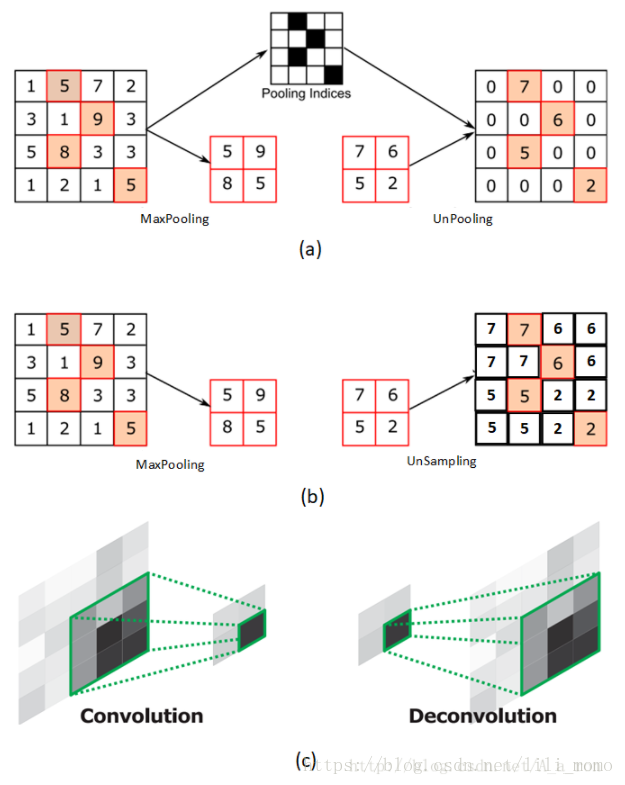
图（a）表示反池化 (unPooling) 的过程，特点是在 Maxpooling 的时候保留最大值的位置信息，之后在 unpooling 阶段使用该信息扩充 feature Map，除最大值位置以外，其余补0。

图（b）表示 unSampling 的过程，与图（a）对应，两者的区别在于 unSampling 阶段没有使用 MaxPooling 时的位置信息，而是直接将内容复制来扩充 feature Map。从图中即可看到两者结果的不同。

图（c）为反卷积 (Deconvolution) 的过程，最大的区别在于反卷积过程是有参数要进行学习的（类似卷积过程），理论是反卷积可以实现 UnPooling 和 unSampling，只要卷积核的参数设置的合理。