正则化

Batch Normalization（批标准化）

• 加速网络的训练（缓解梯度消失，支持更大的学习率）
• 防止过拟合
• 降低了参数初始化的要求

动机

• 训练的本质是学习数据分布。如果训练数据与测试数据的分布不同会降低模型的泛化能力。因此，应该在开始训练前对所有输入数据做归一化处理。
• 而在神经网络中，因为每个隐层的参数不同，会使下一层的输入发生变化，从而导致每一批数据的分布也发生改变；致使网络在每次迭代中都需要拟合不同的数据分布，增大了网络的训练难度与过拟合的风险。

基本原理

BN 方法会针对每一批数据，在网络的每一层输入之前增加归一化处理，使输入的均值为 0，标准差为 1。目的是将数据限制在统一的分布下。

具体来说，针对每层的第 k 个神经元，计算这一批数据在第 k 个神经元的均值与标准差，然后将归一化后的值作为该神经元的激活值。

神经网络中有各种归一化算法：Batch Normalization (BN)、Layer Normalization (LN)、Instance Normalization (IN)、Group Normalization (GN)。从公式看它们都差不多，如 (1) 所示：无非是减去均值，除以标准差，再施以线性映射。

\[y = \gamma \left( \frac { x - \mu ( x ) } { \sigma ( x ) } \right) + \beta\]

这些归一化算法的主要区别在于操作的 feature map 维度不同。如何区分并记住它们，一直是件令人头疼的事。本文目的不是介绍各种归一化方式在理论层面的原理或应用场景，而是结合 pytorch 代码，介绍它们的具体操作，并给出一个方便记忆的类比。

Batch Normalization

Batch Normalization (BN) 是最早出现的，也通常是效果最好的归一化方式。feature map： 包含 N 个样本，每个样本通道数为 C，高为 H，宽为 W。对其求均值和方差时，将在 N、H、W上操作，而保留通道 C 的维度。具体来说，就是把第1个样本的第1个通道，加上第2个样本第1个通道 …… 加上第 N 个样本第1个通道，求平均，得到通道 1 的均值（注意是除以 N×H×W 而不是单纯除以 N，最后得到的是一个代表这个 batch 第1个通道平均值的数字，而不是一个 H×W 的矩阵）。求通道 1 的方差也是同理。对所有通道都施加一遍这个操作，就得到了所有通道的均值和方差。具体公式为：

\[\begin{array} { c } { \mu _ { c } ( x ) = \frac { 1 } { N H W } \sum _ { n = 1 } ^ { N } \sum _ { h = 1 } ^ { H } \sum _ { w = 1 } ^ { W } x _ { n c h w } } \\ { \sigma _ { c } ( x ) = \sqrt { \frac { 1 } { N H W } \sum _ { n = 1 } ^ { N } \sum _ { h = 1 } ^ { H } \sum _ { k = 1 } ^ { W } \left( x _ { n c h w } - \mu _ { c } ( x ) \right) ^ { 2 } + \epsilon } } \end{array}\]

如果把$\boldsymbol { x } \in \mathbb { R } ^ { N \times C \times H \times W }$类比为一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 W 个字符。BN 求均值时，相当于把这些书按页码一一对应地加起来（例如第1本书第36页，第2本书第36页……），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求 “平均书” 的操作（注意这个“平均书”每页只有一个字），求标准差时也是同理。

Layer Normalization

BN 的一个缺点是需要较大的 batchsize 才能合理估训练数据的均值和方差，这导致内存很可能不够用，同时它也很难应用在训练数据长度不同的 RNN 模型上。Layer Normalization (LN) 的一个优势是不需要批训练，在单条数据内部就能归一化。

对于$\boldsymbol { x } \in \mathbb { R } ^ { N \times C \times H \times W }$LN 对每个样本的 C、H、W 维度上的数据求均值和标准差，保留 N 维度。其均值和标准差公式为：

\[\begin{array} { c } { \mu _ { n } ( x ) = \frac { 1 } { C H W } \sum _ { c = 1 } ^ { C } \sum _ { h = 1 } ^ { H } \sum _ { w = 1 } ^ { W } x _ { n c h w } } \\ { \sigma _ { n } ( x ) = \sqrt { \frac { 1 } { C H W } \sum _ { c = 1 } ^ { C } \sum _ { h = 1 } ^ { H } \sum _ { k = 1 } ^ { W } \left( x _ { n c h w } - \mu _ { n } ( x ) \right) ^ { 2 } + \epsilon } } \end{array}\]

继续采用上一节的类比，把一个 batch 的 feature 类比为一摞书。LN 求均值时，相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”，求标准差时也是同理。

Instance Normalization

Instance Normalization (IN) 最初用于图像的风格迁移。作者发现，在生成模型中， feature map 的各个 channel 的均值和方差会影响到最终生成图像的风格，因此可以先把图像在 channel 层面归一化，然后再用目标风格图片对应 channel 的均值和标准差“去归一化”，以期获得目标图片的风格。IN 操作也在单个样本内部进行，不依赖 batch。

对于$x \in \mathbb { R } ^ { N \times C \times H \times W }$，IN 对每个样本的 H、W 维度的数据求均值和标准差，保留 N 、C 维度，也就是说，它只在 channel 内部求均值和标准差，其公式为：

\[\begin{array} { c } { \mu _ { n c } ( x ) = \frac { 1 } { H W } \sum _ { h = 1 } ^ { H } \sum _ { w = 1 } ^ { W } x _ { n c h w } } \\ { \sigma _ { n c } ( x ) = \sqrt { \frac { 1 } { H W } \sum _ { h = 1 } ^ { H } \sum _ { w = 1 } ^ { W } \left( x _ { n c h w } - \mu _ { n c } ( x ) \right) ^ { 2 } + \epsilon } } \end{array}\]

IN 求均值时，相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每页书的“平均字”，求标准差时也是同理。

Group Normalization

Group Normalization (GN) 适用于占用显存比较大的任务，例如图像分割。对这类任务，可能 batchsize 只能是个位数，再大显存就不够用了。而当 batchsize 是个位数时，BN 的表现很差，因为没办法通过几个样本的数据量，来近似总体的均值和标准差。GN 也是独立于 batch 的，它是 LN 和 IN 的折中。正如提出该算法的论文展示的：

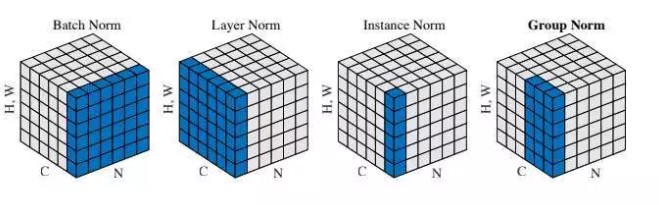
GN 计算均值和标准差时，把每一个样本 feature map 的 channel 分成 G 组，每组将有 C/G 个 channel，然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。

\[\begin{array} { c } { \mu _ { n g } ( x ) = \frac { 1 } { ( C / G ) H W } \sum _ { c = g C / G } ^ { ( q + 1 ) C / G } \sum _ { h = 1 } ^ { H } \sum _ { w = 1 } ^ { W } x _ { n c h w } } \\ { \sigma _ { n g } ( x ) = \sqrt { \frac { 1 } { ( C / G ) H W } } \sum _ { c = g C / C } ^ { ( g + 1 ) C / G } \sum _ { h = 1 } ^ { H } \sum _ { w = 1 } ^ { W } \left( x _ { n c h w } - \mu _ { n g } ( x ) \right) ^ { 2 } + \epsilon } \end{array}\]

继续用书类比。GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，求每个小册子的“平均字”和字的“标准差”。

总结

这里再重复一下上文的类比。如果把$x \in \mathbb { R } ^ { N \times C \times H \times W }$类比为一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 W 个字符。

计算均值时

BN 相当于把这些书按页码一一对应地加起来（例如：第1本书第36页，加第2本书第36页……），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求“平均书”的操作（注意这个“平均书”每页只有一个字）

LN 相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”

IN 相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每页书的“平均字”

GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，对这个 C/G 页的小册子，求每个小册子的“平均字”

计算方差同理

此外，还需要注意它们的映射参数γ和β的区别：对于 BN，IN，GN， 其γ和β都是维度等于通道数 C 的向量。而对于 LN，其γ和β都是维度等于 normalized_shape 的矩阵。

最后，BN和IN 可以设置参数：momentum 和 track_running_stats来获得在全局数据上更准确的 running mean 和 running std。而 LN 和 GN 只能计算当前 batch 内数据的真实均值和标准差。