SVM
转载:https://air-yan.github.io//MachineLearning/sv_svm_ch/
1 直观理解与符号应用
通常,由于二元分类是多元分类中的最简单的情况,人们总是习惯从二元分类下手研究问题。关于二元分类,我们已经在先前的笔记中学过了一些概率模型,例如逻辑回归。至于SVM,它可以对随机空间维度中的点进行分类,并且可以通过使用确定性算法来解决问题。
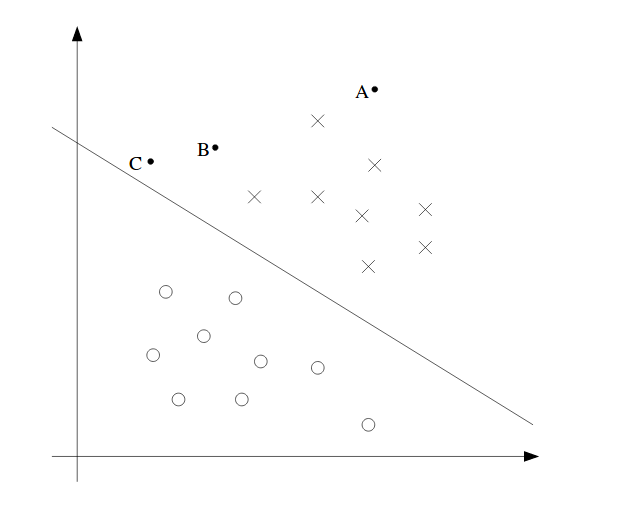
上述2D模型是一个简单的例子。从图中我们可以看到,在空间中有A,B和C点。A是最安全的点,因为它远离边界线(高维的超平面),而C是最危险的点,因为它接近超平面。边界线和点之间的距离称为间隔(margin)。
我们以$x$表示特征向量,以$y$表示分类结果,以$h$表示分类器。因此,SVM分类器可以表示为:
\[h_{w,b}(x) = g(w^Tx + b)\]请注意,SVM和逻辑算法并不一样。在SVM中,w,b代替了原本的$\theta$,而且y的分类结果取值为1和-1,而不是0和1。分类器直接预测结果1或-1,而不像逻辑算法那样计算出概率,这点和感知器算法是一样的。 不过,一些库如Python中的scikit-learn,确实为SVM提供了概率输出。这是通过使用诸如逻辑函数之类的转换函数来实现的。
2 函数间隔与几何间隔
函数间隔关于训练数据的表达:
\[\overset{\wedge}{\gamma^{(i)}} = y^{(i)}(w^Tx^{(i)} + b)\]当分类y为正数1时,我们希望$(w^Tx^{(i)} + b)$是一个较大的正数,当分类为负数-1时,则希望它是一个较大的负数。因此,这意味着函数间隔必须是正数才对。间隔越大,我们就分类的结果越自信。但是当我们将w和b的比例放大到2w和2b而不改变其他任何东西时,这可能并没有什么意义。虽然我们没有因此改变$(w^Tx^{(i)} + b)$的正负符号(也就是预测结果),但我们通过缩放w和b得到了更大的间隔。因此,为了使预测不因w和b的缩放倍数变动而变动,我们接下来将带来一个新的定义 - 几何间隔。此外,我们将数据集的函数间隔表示为:
\[\overset{\wedge}{\gamma} = \min_{i=1,\dots,m} \overset{\wedge}{\gamma^{(i)}}\]其中,m为训练样本的数量。
几何间隔:在几何间隔中,我们认为w和b的缩放倍数大小不应影响间隔的比例,因此需要对w和b进行关于w范数的归一化。一个几何间隔的表示可见下图:
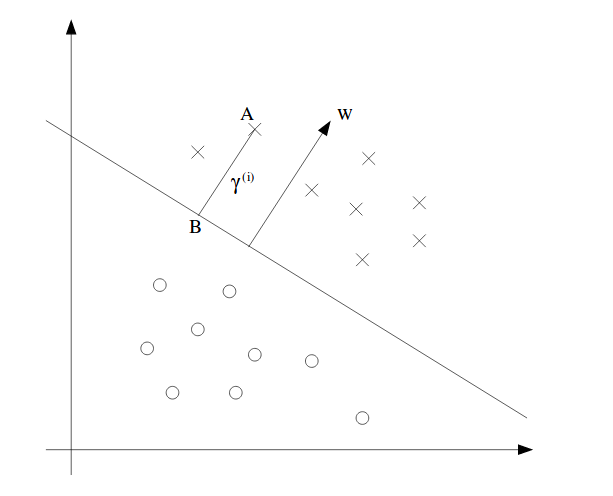
图中w也可以被称为支持向量。w与边界线相垂直,为了证明这一点,让我们在边界线上任取两点$x_i,x_j,i\neq j$。根据定义,我们有:
\[w^T x_i + b = w^T x_j + b = 0\]于是,我们可以有:
\[w^T(x_i-x_j) = 0\]$ x_i-x_j $是沿着边界线的向量。我们知道如果两个向量的点积为零,那么这两个向量是相互垂直的。所以$w^T$与$(x_i-x_j)$互相垂直。
类似地,为了找到A点的间隔,我们声明$\gamma^{(i)}$为一个标量,我们将B点作为A点到边界线的投影点。根据定义,A点到B点可以表示为:$x^{(i)} - \gamma^{(i)} w/\lvert\lvert w \rvert\rvert$。如果这个点是在边界线上的话,可以表示为:
\[w^T(x^{(i)} - \gamma^{(i)} \frac{w}{\lvert\lvert w \rvert\rvert}) + b = 0\]解:
\[\gamma^{(i)} = (\frac{w}{\lvert\lvert w \rvert\rvert})^T x^{(i)} + b/\lvert\lvert w \rvert\rvert\]当然,这仅仅是结果(间隔)为正数的情况。对于负值样本,我们会得到一个负数的结果。所以为了统一这一点,我们将上面推演出的间隔乘以分类y(1或-1)。因此,我们将对于一个训练样本的几何间隔定义为:
\[\gamma^{(i)} = y^{(i)}((\frac{w}{\lvert\lvert w \rvert\rvert})^T x^{(i)} + b/\lvert\lvert w \rvert\rvert)\]如果$\lvert\lvert w \rvert\rvert = 1$,函数间隔则等于几何间隔。几何间隔不会随着w和b的倍数变化而变化,这意味着如果我们将w和b放大2倍,我们将具有相同的几何间隔(不是函数间隔)。这里请注意,我们必须使用相同的标量来缩放两个参数。那么关键点来了,这种情况下,我们想要任何的函数间隔都可以,同时我们仍然可以拥有相同的几何间隔。
类似地,对于所有训练样本的几何间隔是:
\[\gamma = \min_{i=1,\dots,m}\gamma^{(i)}\]3 最优间隔分类器
最重要的是,简单来说,我们的目标是最大化几何间隔,越大越好。
目前,我们假设数据是线性可分的。这个优化问题可以定义为:
\[\max _ { \gamma , w , b } \gamma\] \[\text { s.t. } \quad y ^ { ( i ) } \left( w ^ { T } x ^ { ( i ) } + b \right) \geq \gamma , i = 1 , \ldots , m\] \[\mid w \mid = 1\]第一个约束是确保每个训练样本都具有有效的几何间隔。第二点是为了确保几何间隔等于函数间隔。我们必须有第二个约束,因为 $y^{(i)}(w^Tx^{(i)} + b)$ 是函数间隔。通过第二个约束,我们使得函数间隔等于几何间隔。令人很难受的点是第二个约束 $\lvert\lvert w \rvert\rvert = 1$,使得它不是凸的。如果它是凸的,我们可以对它求导并设它为零来找到极值,但这是另一个话题了。
为此,我们可以将其转换为:
\[\max _ { \gamma , w , b } \gamma\] \[\text { s.t. } \quad y ^ { ( i ) } \left( w ^ { T } x ^ { ( i ) } + b \right) \geq \gamma , i = 1 , \ldots , m\] \[\mid w \mid = 1\]我们使用了函数间隔来表示几何间隔。这里我们用了最初预期的函数间隔,而不是几何间隔。 通过这样做,我们消除了$\lvert\lvert w \rvert\rvert = 1$。但这仍然很糟糕。
回想一下,通过缩放 w 和 b,我们没有改变任何东西。我们使用这个事实来强制函数间隔 $\overset{\wedge}{\gamma} = 1$,而不改变几何间隔。之后,我们的最大值问题现在可以表示为最小值问题:
\[\min _ { \gamma , w , b } \frac { 1 } { 2 } \| w \| ^ { 2 }\] \[\text { s.t. } y ^ { ( i ) } \left( w ^ { T } x ^ { ( i ) } + b \right) \geq 1 , i = 1 , \ldots , m\]同样,我们有$\frac{1}{2}$的原因只是为了数学计算上方便,这并不会制造出任何问题。现在,这个问题已经可以通过使用二次规划软件来解决了,不过我们仍然可以进一步简化这一过程,进一步的简化需要了解拉格朗日对偶性。
4 拉格朗日对偶性
关于如何解决约束优化问题,让我们稍稍插入另一个话题。一般来说,我们通常使用拉格朗日对偶来解决这类问题。我们考虑这样一个问题:
\[\min _ { w } f ( w )\] \[\text { s.t. } h _ { i } ( w ) = 0 , i = 1 , \ldots , l\]现在,我们可以将拉格朗日定义为:
\[\mathcal{L}(w,\beta) = f(w) + \sum\limits_{i=1}^l \beta_i h_i(w)\]其中$\beta_i$称为拉格朗日乘数。现在,我们可以求偏导数并设为零,并找出每个$w_i$和每个$\beta_i$。
上述只有等式约束,同时我们可以推演到等式和不等式约束。所以我们定义 Primal Problem 为:
\[\min _ { w } f ( w )\] \[\text { s.t. } g _ { i } ( w ) \leq 0 , i = 1 , \ldots , k\] \[\qquad h _ { i } ( w ) = 0 , i = 1 , \ldots , l\]我们将广义拉格朗日定义为:
\[\mathcal { L } = f ( w ) + \sum _ { i = 1 } ^ { k } \alpha _ { i } g _ { i } ( w ) + \sum _ { i = 1 } ^ { l } \beta _ { i } h _ { i } ( w )\]其中所有的 $\alpha$和$\beta$ 都是拉格朗日乘子。
让我们定义 primal problem 的数量为:
\[\theta_{\mathcal{P}}(w) = \max_{\alpha,\beta:\alpha_i\geq 0} \mathcal{L}(w,\alpha,\beta)\]在这个数量中,我们需要$\alpha_i$大于零。如果$\alpha_i < 0$,则由于$g_i(w) \leq 0$,则上述量的最大值就是$\infty$。此外,如果违反了某些约束,那么我们也将得到$\theta_{\mathcal{P}}(w) = \infty$。
如果所有条件都满足的话,我们将有:
为了与我们的 primal problem 相匹配,我们将最小问题定义为:
\[\min_w \theta_{\mathcal{P}}(w) = \min_w \max_{\alpha,\beta:\alpha_i\geq 0} \mathcal{L}(w,\alpha,\beta)\]如果满足了所有约束,那么这将与 primal problem 相同。我们将 primal problem 的值定义为:$p^{\ast} = \min_w \theta_{\mathcal{P}(w)}$
从不同的角度我们可以将以下定义为 dual problem(对偶问题)的一部分:
\[\theta_{\mathcal{D}}(\alpha,\beta) = \min_w \mathcal{L}(w,\alpha,\beta)\]为了再次与 primal problem 相匹配,我们将对偶最优化问题 (dual optimization problem) 定义为:
\[\max_{\beta,\alpha:\alpha_i\geq 0} \theta_{\mathcal{D}}(\alpha,\beta) = \max_{\alpha,\beta:\alpha_i\geq 0} \min_w \mathcal{L}(w,\alpha,\beta)\]相同的,对偶问题的值为:$d^{\ast} = \max_{\alpha,\beta:\alpha_i\geq 0} \theta_{\mathcal{D}}(\alpha,\beta)$
Primal 和 dual problem 的相关性为:
\[d^{\ast} = \max_{\alpha,\beta:\alpha_i\geq 0} \theta_{\mathcal{D}}(\alpha,\beta) \leq p^{\ast} = \min_w \theta_{\mathcal{P}(w)}\]上述公式永远为真。要证明这一点,我们首先定义一个函数$f(x,y): X \times Y \mapsto \mathbb{R}$。然后,我们可以定义:
\[g(x) := \min_{y} f(x,y)\]也就是说,对于函数g的每个x,我们选一个能使f(x,y)最小化的y值。然后,我们可以说:
\[g(x) \leq f(x,y) \forall x\forall y\]我们可以在两边各添加一个max运算符,以消除变量x:
\[\max_{x} g(x) \leq \max_{x} f(x,y) \forall y\]这等同于:
\[\max_{x} \min_{y} f(x,y) \leq \min_{y} \max_{x} f(x,y)\]以上便是证明的过程。
回到主题:关键是在某些条件下,它们是相等的。如果他们是相等的,我们可以专注于dual problem而不是primal problem。那么唯一的问题将是 - 它们何时相等。
我们假设f和g都是凸函数,h是仿射函数(当f有Hessian时,如果Hessian是正半正定则它是凸的。所有仿射都是凸的,仿射意味着线性。),对于一些w,函数g全部小于0。
从这些假设出发,primal的解$w^{\ast}$一定存在,dual的解$\alpha^{\ast},\beta^{\ast}$一定存在,同时$p^{\ast} = d^{\ast}$,并且$w^{\ast}$,$\alpha^{\ast}$和$\beta^{\ast}$满足 Karush-Kuhn-Tucker(KKT)条件,KKT条件是:
\[\frac { \partial } { \partial w _ { i } } \mathcal { L } \left( w ^ { * } , \alpha ^ { * } , \beta _ { * } \right) = 0 , \qquad i = 1 , \ldots , n\] \[\frac { \partial } { \partial \beta _ { i } } \mathcal { L } \left( w ^ { * } , \alpha ^ { * } , \beta _ { * } \right) = 0 ,\qquad i = 1 , \ldots , l\] \[\alpha _ { i } ^ { * } g _ { i } \left( w ^ { * } \right) \leq 0 ,\qquad \quad i = 1 , \ldots , k\] \[g _ { i } \left( w ^ { * } \right) \leq 0 ,\qquad \qquad i = 1 , \ldots , k\]第三个等式被称为KKT dual complementarity condition。意思是如果$\alpha_i^{\ast} > 0$,那么$g_i(w^{\ast}) = 0$。当primal problem等于dual problem时,上述的每个条件和假设都会成立。
5 最优间隔分类器
让我们回到SVM的primal problem:
\[\min _ { \gamma , w , b } \frac { 1 } { 2 } \| w \| ^ { 2 }\] \[\text { s.t. } y ^ { ( i ) } \left( w ^ { T } x ^ { ( i ) } + b \right) \geq 1 , i = 1 , \ldots , m\]我们可以重新设定约束为:
\[g_i(w) = -y^{(i)}(w^Tx^{(i)} + b) + 1 \leq 0\]其中i包含所有训练样本。从KKT条件中我们可以看到,当函数间隔为1且$g_i(w) = 0$时,$\alpha_i > 0$。
我们可以在下面的图片中看到这一点:虚线上的三个点是具有最小几何间隔的点,所以这些点的$\alpha_i$为正值。这些点也被称为支持向量。
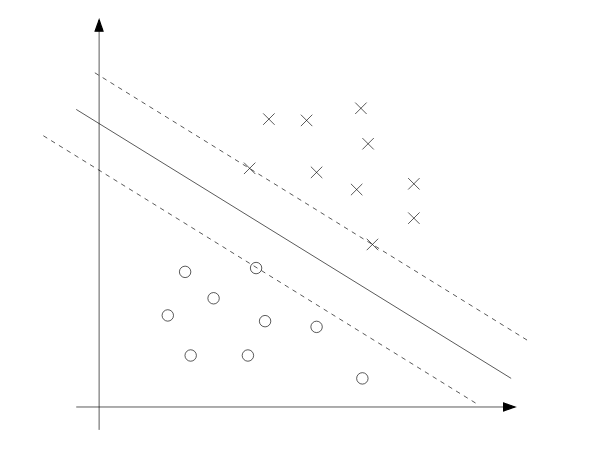
仅有不等式约束的拉格朗日:
\[\mathcal{L}(w,b,\alpha) = \frac{1}{2}\lvert \lvert w\rvert \rvert^2 - \sum\limits_{i=1}^m \alpha_i [y^{(i)}(w^Tx^{(i)} + b) - 1] \tag{1}\]要找到这个问题的对偶形式(dual form)的话,我们需要在给定$\alpha$的情况下,找到损失函数中w和b的最小值:
对于 w:
\[\triangledown_{w}\mathcal{L}(w,b,\alpha) = w - \sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)} = 0\tag{2}\]这说明:
\[w = \sum\limits_{i=1}^m \alpha_i y^{(i)}x^{(i)}\tag{3}\]对于 b:
\[\frac{\partial}{\partial b}\mathcal{L}(w,b,\alpha) = \sum\limits_{i=1}^m \alpha_i y^{(i)} = 0 \tag{4}\]一个有用的公式:
\[\left\| \sum _ { i = 1 } ^ { m } \alpha _ { i } y ^ { ( i ) } x ^ { ( i ) } \right\| ^ { 2 } = \left( \sum _ { i = 1 } ^ { m } \alpha _ { i } y ^ { ( i ) } x ^ { ( i ) } \right) ^ { T } \left( \sum _ { i = 1 } ^ { m } \alpha _ { i } y ^ { ( i ) } x ^ { ( i ) } \right)\] \[\qquad \qquad = \sum _ { i , j } ^ { m } y ^ { ( i ) } y ^ { ( j ) } \alpha _ { i } \alpha _ { j } \left( x ^ { ( i ) } \right) ^ { T } x ^ { ( j ) }\]我们将等式(3)带回到等式(1),得到:
\[\mathcal { L } ( w , b , \alpha ) = \frac { 1 } { 2 } \sum _ { i , j } ^ { m } y ^ { ( i ) } y ^ { ( j ) } \alpha _ { i } \alpha _ { j } \left( x ^ { ( i ) } \right) ^ { T } x ^ { ( j ) } - \sum _ { i = 1 } ^ { m } \alpha _ { i } \left[ y ^ { ( i ) } \left( \left( \sum _ { j = 1 } ^ { m } \alpha _ { j } y ^ { ( j ) } x ^ { ( j ) } \right) ^ { T } x ^ { ( i ) } + b \right) - 1 \right]\] \[\qquad \quad \quad = \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} - \sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)} - b\sum\limits_{i=1}^m\alpha_i y^{(i)} + \sum\limits_{i=1}^m \alpha_i\] \[= \sum\limits_{i=1}^m \alpha_i - \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j (x^{(i)})^Tx^{(j)}\]我们需要注意$\alpha_i \geq 0$ 和约束(4)。因此,我们得到的dual problem为:
\[\max_{\alpha} W(\alpha) = \sum\limits_{i=1}^m \alpha_i - \frac{1}{2}\sum\limits_{i,j}^m y^{(i)}y^{(j)}\alpha_i\alpha_j <x^{(i)},x^{(j)}>\] \[\text{s.t. } \quad \alpha_i \geq 0, i = 1,\dots,m\] \[\sum\limits_{i=1}^m \alpha_i y^{(i)} = 0\]这是满足KKT条件的,可以自己尝试着去证明一下。这意味着我们现在要解决的是dual problem而不是primal problem。如果我们可以在这个dual problem中找到$\alpha$,我们就可以用等式(3)去找到$w^{\ast}$。有了最优化的$w^{\ast}$,我们可以找到$b^{\ast}$:
\[b^{\ast} = -\frac{\max_{i:y^{(i)}=-1}w^{\ast T}x^{(i)} + \min_{i:y^{(i)}=1}w^{\ast T}x^{(i)}}{2}\]想验证它的话很容易。基本上我们要做的就是,分别从正负两个类别中取出与超平面具有相同距离的点,也就是支持向量。由于它们的间隔是相同的,我们可以很好的用这个属性来解$b^{\ast}$。将w和b最优化后,最近的正负样本的几何间隔将会相等。
等式(3)所表达的是:最优化的w是基于最优化的$\alpha$的。为了做出预测,我们可以:
\[w^Tx + b = (\sum\limits_{i=1}^m \alpha_i y^{(i)} x^{(i)})^Tx + b = \sum\limits_{i=1}^m \alpha_i y^{(i)} <x^{(i)},x> + b\]如果大于零,我们预测1,小于零则预测-1。我们知道,由于约束,除了支持向量以外的所有$\alpha$将为零。这意味着我们只关心x与支持向量的内积。这使得预测更快并且将核函数概念带入我们的讨论中。请记住,到目前为止,一切都是低维度的。那么高维度和无限维度空间将会是什么情况呢?
6 核函数
在房屋居住区域的例子中,我们可以使用特征$x,x^2,x^3$来获得三维函数,其中$x$可以是房屋的大小。 我们称$x$为输入属性,$x,x^2,x^3$,称为特征。我们声明一个特征映射函数$\phi (x)$,这个函数可以将输入属性映射到特征。
因此,我们可以在新的特征空间$\phi (x)$中进行训练学习。在上一节结尾我们了解了,需要计算内积$<x,z>$。现在我们可以用$<\phi(x),\phi(z)>$替换它。
定义上讲,给定一个映射函数我们可以将核函数声明为:
\[K(x,z) = \phi(x)^T\phi(z)\]这里我们可以使用核函数,而不是映射函数本身,其原因可以在cs229课程的原笔记中找到,由于内容比较细节这里就不再过多赘述。简而言之,核函数在计算上复杂度较低,并且可以用于高维度或无限维度映射中。所以我们可以在高维空间中进行训练而无需计算映射函数$\phi$。
原笔记中有一个例子证明了核函数的效率之高。你需要知道的是,计算映射所需要的时间复杂度是呈指数的,而计算核函数需要的时间复杂度是线性的。
换句话说,核函数是用来计算两个样本(x 和 z)之间的远近的,它呈现了相似性的概念。在流行的核函数中,有一个被称为高斯核函数,其定义如下:
\[K(x,z) = \exp(-\frac{\lvert\lvert x-z \rvert\rvert^2}{2\sigma^2})\]我们可以使用它来训练SVM,它对应的是无限维度特征映射函数$\phi$。这意味着映射函数$\phi$是无限维度的。计算机是无法计算无线维度上的映射函数的,但我们可以使用核函数来直接得出对于应的內积值。
接下来,我很想讨论下关于核函数有效性的事情。
我们定义拥有m个点的核矩阵为$K_{ij} = K(x^{(i)},x^{(j)})$ K是 m x m 矩阵。那么现在,如果K是有效的话,这意味着:
(1)对称矩阵: $K_{ij} = K(x^{(i)},x^{(j)}) = \phi(x^{(i)})^T\phi(x^{(j)}) = \phi(x^{(j)})^T\phi(x^{(i)}) = K_{ji}$
(2)半正定矩阵: $z^TKz \geq 0$ 这个证明很简单,如果需要的话可以提供过程。
Mercer定理(Mercer Theorem的中文无对应翻译):设$K:\mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}$。为了使核函数有效,对于任何${x^{(1)},\dots,x^{(m)}}$,对应的核矩阵必须同时是对称的,也是半正定的,这是一个充要条件。
核函数方法不仅在SVM中有运用,它在任何有内积的情况下都是用途颇广的。因此,我们用核函数替换内积,以便在更高的维度空间中使用。
7 正规化与无法分割问题
尽管将x映射到更高维度的空间增加了可分离的机会,但情况可能并非总是如此。一个异常值的出现也是非常棘手的,我们不会想把这种异常值放入训练集的。下图演示了这种情况:
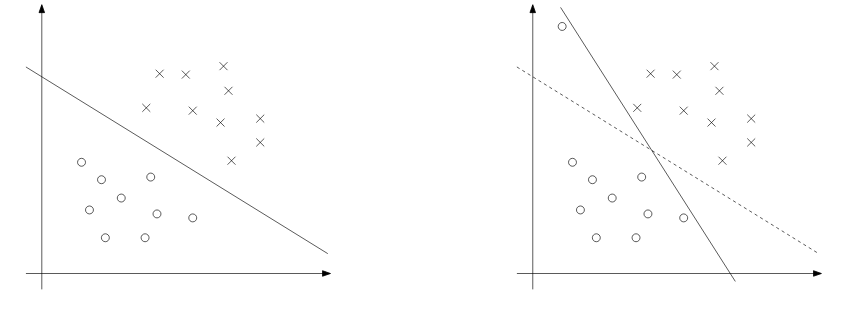
为了使算法也适用于非线性情况,我们将用到正则化:
正规化将惩罚对于函数间隔小于1的样本,C将确保大多数样本的函数间隔至少为1。这表明了:
(1) 我们希望w小,这样间隔就会大。
(2) 我们希望大多数样本的函数间隔大于1。
拉格朗日为:
\[\mathcal{L}(w,b,\xi,\alpha,r) = \frac{1}{2}w^Tw + C\sum\limits_{i=1}^{m}\xi_i - \sum\limits_{i=1}^m \alpha_i[y^{(i)}(x^{(i)T}w + b) - 1 + \xi_i] - \sum\limits_{i=1}^{m}r_i\xi_i\]其中 $\alpha$ 和 r 是拉格朗日乘数。因为这里的约束是不等式约束,所以这些乘数不能是负数。现在,我们需要做同样的事情来找出 dual problem 的形式,这里的过程我也不再赘述了。在将 w 和 b 的导数设为零之后,带回后得到 dual problem:
\[\max_{\alpha} W(\alpha) = \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i,j=1}^{m}y^{(i)}y^{(j)}\alpha_i\alpha_j<x^{(i)},x^{(j)}>\] \[\text{s.t. }0\leq \alpha_i \leq C,i=1,\dots,m\] \[\sum\limits_{i=1}^{m}\alpha_i y^{(i)} = 0\]注意,$\alpha$ 的值有一个区间。这是因为 $\sum\limits_{i=1}^{m}(C-\alpha_i-r_i)\xi_i$。我们将 $\xi$ 取导并设零,将得到的结果带回原等式消除 $\xi$,我们便得到了 $\alpha$ 的区间。在这个情况下,当 $r_i = 0$ 时,$r_i$ 始终为非负数,$\alpha_i=C$。
还需要注意的是,由于两个最近的点的间隔都已改变,这里的最优b不再与之前相同。在下一节中,我们将找到一个合适的算法来解决问题。
8 序列最小优化算法(SMO)
John Platt的SMO(顺序最小优化)算法的出现是用来解决SVM中的dual problem的。
8.1 坐标上升法
一般来讲,最优化问题
\[\max_{\alpha}W(\alpha_1,\alpha_2,\dots,\alpha_m)\]可以通过梯度上升和牛顿法来解决。另外,我们也可以使用坐标上升法:
<figure class="highlight"><pre><code class="language-bash" data-lang="bash"><span class="k">for </span>loop <span class="k">until </span>convergence:
<span class="k">for </span>i <span class="k">in </span>range<span class="o">(</span>1,m<span class="o">)</span>:
alpha<span class="o">(</span>i<span class="o">)</span> <span class="o">=</span> argmin of alpha<span class="o">(</span>i<span class="o">)</span> W<span class="o">(</span>all alpha<span class="o">)</span></code></pre></figure>
总的来说,我们将除$\alpha_i$之外的所有$\alpha$固定,然后移动到下一个$\alpha$进行更新。 假设计算$\alpha$的梯度是有效的。举个例子:
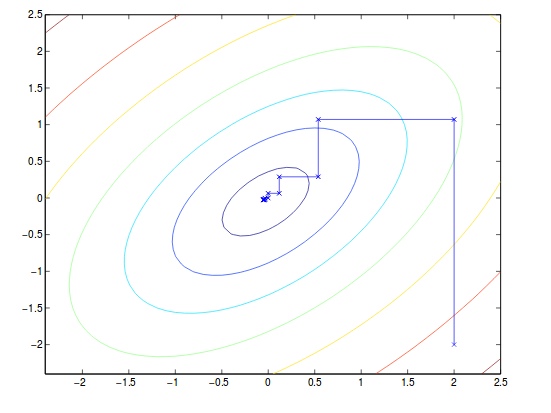
这里请注意,收敛的路径始终与x或y轴平行,因为它每一次只更新一个变量。
8.2 序列最小优化算法(SMO)
我们不能在SVM的dual problem中做与上面相似的事情,因为只改变一个变量可能会违反约束:
\[\alpha_1 y^{(1)} = -\sum\limits_{i=2}^m \alpha_i y^{(i)}\]这表示一旦我们确定剩余部分的$\alpha$,我们就不能再改变左边的$\alpha$了。因此,我们必须一次性改变两个$\alpha$并更新它们。例如,我们可以:
\[\alpha_1 y^{(1)} + \alpha_2 y^{(2)} = -\sum\limits_{i=3}^m \alpha_i y^{(i)}\]我们使右边保持不变:
\[\alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta\]在图中可以表示为:
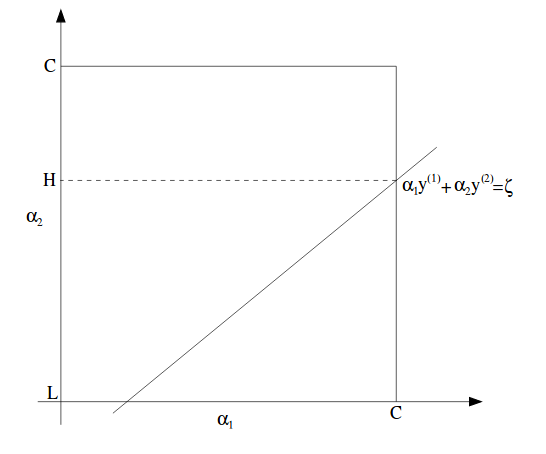
在此图中,L和H是$\alpha_2$可能达到的最低值和最高值,而$\alpha_1$介于0和C之间。
这里注意,尽管$\alpha$是在这个正方形中的,不过给定一条直线,它们的上下限会有所限制。
我们可以重写上面的等式:
\[\alpha_1 = (\zeta - \alpha_2 y^{(2)})y^{(1)}\]那么W将会是:
\[W(\alpha_1,\dots,\alpha_m) = W((\zeta-\alpha_2 y^{(2)})y^{(1)},\alpha_2,\dots,\alpha_m)\]我们将所有其他$\alpha$视为常量。因此,带入等式后W将变为二次函数,对于某些a,b和c,可以写为$a\alpha_2^2 + b\alpha_2 + c$。
最后,我们将 $\alpha_2^{new, unclipped}$ 定义为用来更新$\alpha_2$的解决方案。因此,通过针对这一个变量应用约束,我们可以得到: