贝叶斯原理及其推断
贝叶斯定理
条件概率:在时间 B 发生的情况下,事件 A 发生的概率,用 $P \left( A \mid B \right)$ 来表示。
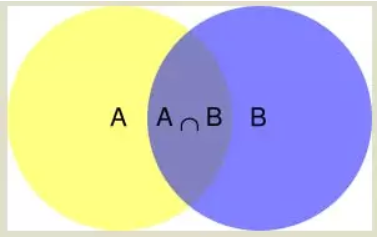
根据文氏图,可以很清楚的看到在事件 B 发生的情况下,事件 A 发生的概率就是 P(AB) 除以 P(B)。
\[P ( A \mid B ) = \frac { P ( A \cap B ) } { P ( B ) }\] \[\Rightarrow P ( A \cap B ) = P ( A \mid B ) P ( B )\] \[\Rightarrow P ( A \mid B ) P ( B ) = P ( B \mid A ) P ( A )\]条件概率计算公式
\[\Rightarrow P ( A \mid B ) = \frac { P ( B \mid A ) P ( A ) } { P ( B ) }\]全概率公式
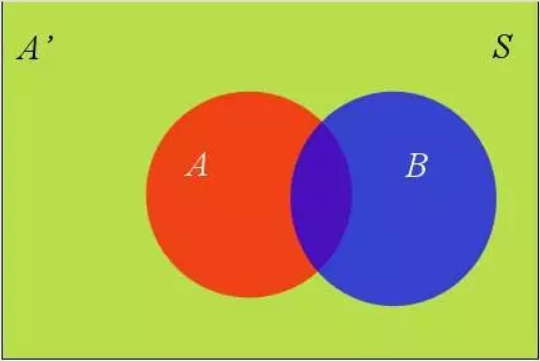
假定样本空间 S,是两个事件 A 和 A’ 的和。

上图中,红色部分是事件 A,绿色部分是事件 A’,它们共同构成了样本空间 S。 在这种情况下,事件 B 可以划分为两个部分。
含义:如果 A 和 A’ 构成样本空间的一个划分,那么事件B的概率,就等于 A 和 A’ 的概率分别乘以 B 对这两个事件的条件概率之和。
\[P ( A \mid B ) = \frac { P ( B \mid A ) P ( A ) } { P ( B \mid A ) P ( A ) + P \left( B \mid A ^ { \prime } \right) P \left( A ^ { \prime } \right) } \qquad \text 全概率公式\]贝叶斯推断的含义
对条件概率公式进行变形,可以得到如下形式:
\[P ( A \mid B ) = P ( A ) \frac { P ( B \mid A ) } { P ( B ) }\]我们把 P(A) 称为”先验概率”,即在B事件发生之前,我们对A事件概率的一个判断。P(A|B) 称为”后验概率”,即在事件 B 发生之后,我们队 A 事件的重新评估。P(B|A)/P(B) 称为”可能性函数”,这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解为下面的式子:
\[\text {后验概率} = \text {先验概率} \times \text {调整因子}\]这就是贝叶斯推断的含义。我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是消弱了”先验概率”,由此得到更接近事实的”后验概率”。