SPP 笔记

1. 基础框架
CNN网络需要固定尺寸的图像输入,SPPNet将任意大小的图像池化生成固定长度的图像表示,提升R-CNN检测的速度24-102倍。
固定图像尺寸输入的问题,截取的区域未涵盖整个目标或者缩放带来图像的扭曲。
事实上,CNN的卷积层不需要固定尺寸的图像,全连接层是需要固定大小输入的,因此提出了SPP层放到卷积层的后面,改进后的网络如下图所示:

SPP是BOW的扩展,将图像从精细空间划分到粗糙空间,之后将局部特征聚集。在CNN成为主流之前,SPP在检测和分类的应用比较广泛。
2. SPP的优点
-
任意尺寸输入,固定大小输出
-
层多
-
可对任意尺度提取的特征进行池化
3. 原图中的ROI如何映射到feature map
3.1 感受野
卷积神经网络CNN中,某一层输出结果中一个元素所对应的输入层的区域大小,被称作感受野receptive field。感受野的大小是由kernel size,stride,padding , outputsize 一起决定的。
output field size = ( input field size - kernel size + 2 * padding ) / stride + 1
(output field size 是卷积层的输出,input field size 是卷积层的输入)
反过来:input field size = (output field size - 1)* stride - 2 * padding + kernel size
一般化公式:
Convolution/Pooling layer:$p_{i} = s_{i} \cdot p_{i+1} + \left ( \left ( k_{i}-1 \right ) / 2 - \text{padding} \right )$
Neuronlayer(ReLU/Sigmoid/..):$p_{I} = p_{i+1}$
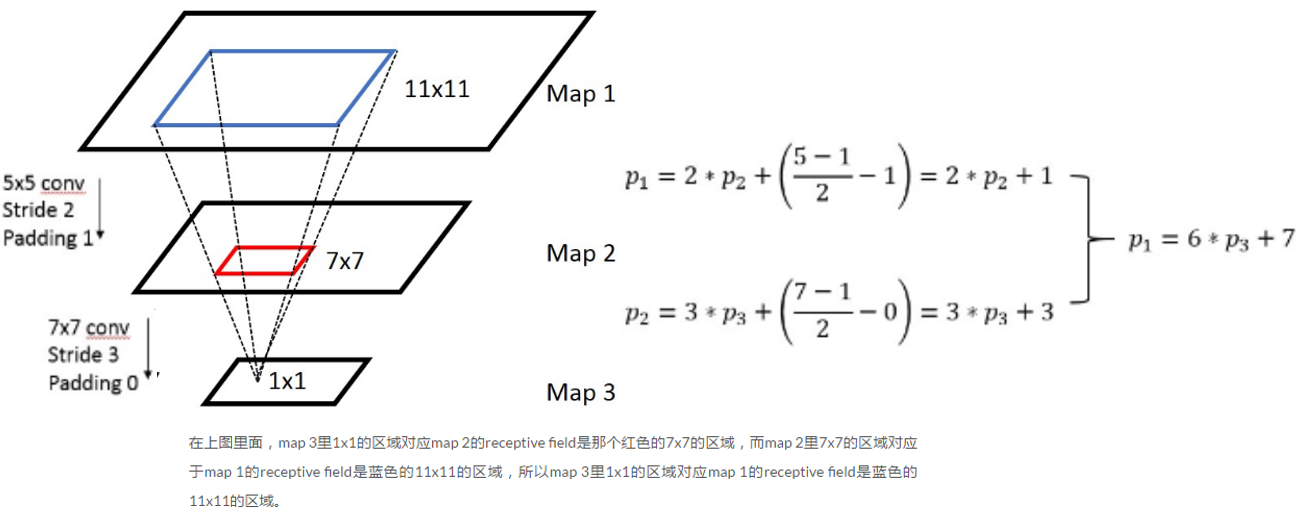
3.2 映射
SPP-net 是把原始ROI的左上角和右下角 映射到 feature map上的两个对应点。 有了feature map上的两队角点就确定了 对应的 feature map 区域(下图中橙色)。
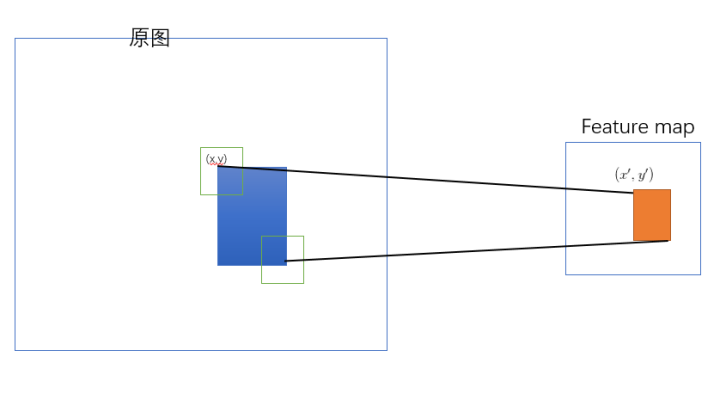
3.2.1 如何映射?
左上角的点(x,y)映射到 feature map上的(x’, y’) : 使得 (x’, y’) 在原始图上感受野(上图绿色框)的中心点 与(x, y)尽可能接近。
3.2.2 对应点之间的映射公式是啥?
就是前面每层都填充 padding/2 得到的简化公式 :
\[p_{i} = s_{i} \cdot p_{i+1}\]需要把上面公式进行级联得到
\[p_{0} = S \cdot p_{i+1}\]其中
\[S = \prod_{0}^{i}s_{i}\]对于feature map 上的 $\left ( x^{‘}, y^{‘} \right )$ 它在原始图的对应点为 $\left ( x^{‘}, y^{‘} \right ) = \left ( Sx^{‘}, Sy^{‘} \right )$。
论文中的最后做法:
把原始图片中的ROI映射为 feature map中的映射区域(上图橙色区域)其中
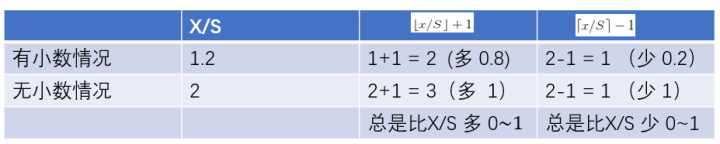
左上角取:$x^{‘}=\left \lfloor x/S \right \rfloor + 1, y^{‘}=\left \lfloor y/S \right \rfloor + 1$
右下角的点取:$x^{‘}=\left \lceil x/S \right \rceil - 1, y^{‘}=\left \lceil y/S \right \rceil - 1$
$\left \lfloor x/S \right \rfloor + 1,\left \lceil x/S \right \rceil - 1$的作用效果分别是增加和减少。也就是 左上角要向右下偏移,右下角要想要向左上偏移。
采取这样的策略是因为论文中的映射方法(左上右下映射)会导致 feature map 上的区域反映射回原始ROI时有多余的区域(下图左边红色框是比蓝色区域大的)
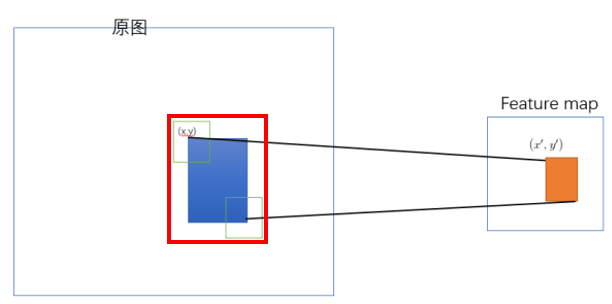
4. 理解池化
R-CNN提取特征比较耗时,需要对每个warp的区域进行学习,而SPPNet只对图像进行一次卷积,之后使用SPPNet在特征图上提取特征。结合EdgeBoxes提取的proposal,
系统处理一幅图像需要0.5s。SPP层的结构如下,将紧跟最后一个卷积层的池化层使用SPP代替,输出向量大小为kM,k=#filters,M=#bins,作为全连接层的输入。
至此,网络不仅可对任意长宽比的图像进行处理,而且可对任意尺度的图像进行处理。尺度在深层网络学习中也很重要。
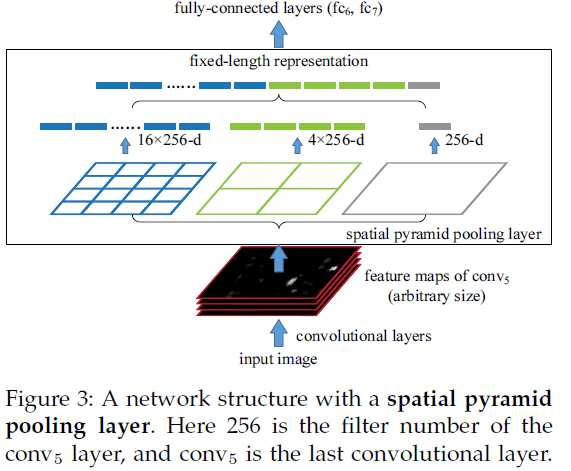
假设原图输入是224x224,对于conv5出来后的输出是13x13x256的,可以理解成有256个这样的filter,每个filter对应一张13x13的reponse map。
如果像上图那样将reponse map分成1x1(金字塔底座),2x2(金字塔中间),4x4(金字塔顶座)三张子图,分别做max pooling后,出来的特征就是(16+4+1)x256 维度。
如果原图的输入不是224x224,出来的特征依然是(16+4+1)x256维度。这样就实现了不管图像尺寸如何 池化n 的输出永远是 (16+4+1)x256 维度。
实际运用中只需要根据全连接层的输入维度要求设计好空间金字塔即可。
5. 网络训练
-
multi-size训练,输入尺寸在[180,224]之间,假设最后一个卷积层的输出大小为 a x a ,若给定金字塔层有 n x n 个bins,进行滑动窗池化,窗口尺寸为 win = [a/n],步长为 str = [a/n],使用一个网络完成一个完整epoch的训练,之后切换到另外一个网络。只是在训练的时候用到多尺寸,测试时直接将SPPNet应用于任意尺寸的图像。
-
如果原图输入是224x224,对于conv5出来后的输出,是13x13x256的,可以理解成有256个这样的filter,每个filter对应一张13x13的reponse map。如果像上图那样将reponse map分成4x4 2x2 1x1三张子图,做max pooling后,出来的特征就是固定长度的(16+4+1)x256那么多的维度了。如果原图的输入不是224x224,出来的特征依然是(16+4+1)x256。
直觉地说,可以理解成将原来固定大小为(3x3)窗口的pool5改成了自适应窗口大小,窗口的大小和reponse map成比例,保证了经过pooling后出来的feature的长度是一致的。
6. 结论
输入层:一张任意大小的图片,假设其大小为(w,h)。
输出层:21个神经元。
也就是我们输入一张任意大小的特征图的时候,我们希望提取出21个特征。空间金字塔特征提取的过程如下:

如上图所示,当我们输入一张图片的时候,我们利用不同大小的刻度,对一张图片进行了划分。 上面示意图中,利用了三种不同大小的刻度,对一张输入的图片进行了划分,最后总共可以得到16+4+1=21个块,我们即将从这21个块中,每个块提取出一个特征,这样刚好就是我们要提取的21维特征向量。
-
第一张图片,我们把一张完整的图片,分成了16个块,也就是每个块的大小就是(w/4, h/4);
-
第二张图片,划分了4个块,每个块的大小就是 (w/2, h/2);
-
第三张图片,把一整张图片作为了一个块,也就是块的大小为 (w, h)
空间金字塔最大池化的过程,其实就是从这21个图片块中,分别计算每个块的最大值,从而得到一个输出神经元。最后把一张任意大小的图片转换成了一个固定大小的21维特征(当然你可以设计其它维数的输出,增加金字塔的层数,或者改变划分网格的大小)。
上面的三种不同刻度的划分,每一种刻度我们称之为:金字塔的一层,每一个图片块大小我们称之为:windows size了。如果你希望,金字塔的某一层输出n*n个特征,那么你就要用windows size大小为:(w/n,h/n) 进行池化了。当我们有很多层网络的时候,当网络输入的是一张任意大小的图片,这个时候我们可以一直进行卷积、池化,直到网络的倒数几层的时候,也就是我们即将与全连接层连接的时候,就要使用金字塔池化,使得任意大小的特征图都能够转换成固定大小的特征向量,这就是空间金字塔池化的奥义(多尺度特征提取出固定大小的特征向量)。